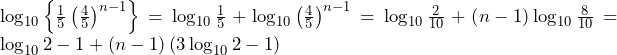方針の立て方 (ⅰ) 全体的に,実際に題意を満たす取り出し方を考えることで方針を得られる.数字によって,玉の個数に偏り(例えば数字5の書かれた玉は1個しかないが,数字2の書かれた玉は3個ある)があるため,場合分けは玉に書かれた数字で行うのが良いだろうと考える. (ⅱ) 今度は個数の問題になっているた
- …続きを読む
- 方針の立て方
(ⅰ)
全体的に,実際に題意を満たす取り出し方を考えることで方針を得られる.数字によって,玉の個数に偏り(例えば数字5の書かれた玉は1個しかないが,数字2の書かれた玉は3個ある)があるため,場合分けは玉に書かれた数字で行うのが良いだろうと考える.(ⅱ)
今度は個数の問題になっているため太郎が何個の玉を獲得するのかで場合分けを行う.(ⅲ)
今度は色の問題になっているため,色で場合分けを行う.後半はやや解法が立てにくいが実際に題意を満たす場合を考えると,花子が4個獲得する必要があることや玉に書かれた数の和が15となるパターンが少ないことが分かり,虱潰し的に考えつくせば良いと判断できる.解説
1回のゲームにおける玉の取り出し方の総数は, 通り.
通り.
(ⅰ)
〇太郎が1個の玉を獲得する確率((40)~(42)について)
題意を満たすには,太郎と花子が同じ数の書かれた玉を取り出せば必要十分.
2人が1の書かれた玉を取り出し,題意を満たす場合の数は, 通り.
通り.
2人が2の書かれた玉を取り出し,題意を満たす場合の数は, 通り.
通り.
2人が3の書かれた玉を取り出し,題意を満たす場合の数は, 通り.
通り.
2人が4の書かれた玉を取り出し,題意を満たす場合の数は, 通り.
通り.
よって,題意を満たす場合の数は, 通り.
通り.
よって,太郎が1個の玉を獲得する確率は, ……(答)
……(答)
〇花子が2個の玉を獲得する確率((43)~(46)について)
題意を満たすには,太郎の取り出した玉の数より,花子の取り出した玉の数が大きければ必要十分.
(Ⅰ)太郎が1の書かれた玉を取り出した場合(太郎がどの色を取り出すかで3通りある)
題意を満たす花子の玉の取り出し方の場合の数は,9通り.
(Ⅱ)太郎が2の書かれた玉を取り出した場合(太郎がどの色を取り出すかで3通りある)
題意を満たす花子の玉の取り出し方の場合の数は,6通り.
(Ⅲ)太郎が3の書かれた玉を取り出した場合(太郎がどの色を取り出すかで3通りある)
題意を満たす花子の玉の取り出し方の場合の数は,3通り.
(Ⅳ)太郎が4の書かれた玉を取り出した場合(太郎がどの色を取り出すかで2通りある)
題意を満たす花子の玉の取り出し方の場合の数は,1通り.
以上,(Ⅰ)~(Ⅳ)より,題意を満たす場合の数は, 通り.
通り.
よって,花子が2個の玉を獲得する確率は, ……(答)
……(答)
〇 ((47)~(51)について)
((47)~(51)について)
確率 は,「花子が2個の玉を獲得した」という条件のもとで,「玉に書かれた数の差の絶対値が
は,「花子が2個の玉を獲得した」という条件のもとで,「玉に書かれた数の差の絶対値が である」という事象が起こる条件付き確率である.
である」という事象が起こる条件付き確率である.
(Ⅰ)花子が2個の玉を獲得し,かつ玉に書かれた数の差の絶対値が1である確率
太郎と花子の取り出した玉に書かれている数字が のいずれかである場合の確率である.よって,確率は,
のいずれかである場合の確率である.よって,確率は,

(Ⅱ)花子が2個の玉を獲得し,かつ玉に書かれた数の差の絶対値が2である確率
太郎と花子の取り出した玉に書かれている数字が のいずれかである場合の確率である.よって,確率は,
のいずれかである場合の確率である.よって,確率は,

(Ⅲ)花子が2個の玉を獲得し,かつ玉に書かれた数の差の絶対値が3である確率
太郎と花子の取り出した玉に書かれている数字が のいずれかである場合の確率である.よって,確率は,
のいずれかである場合の確率である.よって,確率は,

(Ⅳ)花子が2個の玉を獲得し,かつ玉に書かれた数の差の絶対値が4である確率
太郎と花子の取り出した玉に書かれている数字が である場合の確率である.よって,確率は,
である場合の確率である.よって,確率は,

以上,(Ⅰ)~(Ⅳ)と,花子が2個の玉を獲得する確率は であることから,
であることから,

となる.
 ……(答)
……(答)(ⅱ)
(Ⅰ)太郎が1個も玉を獲得しなかった場合
題意を満たす取り出し方は存在しない.
(Ⅱ)太郎が1個の玉を獲得した場合
題意を満たす取り出し方は,「太郎が赤の1,2,3,4の玉いずれかを取り出し,かつ花子が同じ数字の玉を取り出す」である.この取り出し方の場合の数は, 通り.
通り.
(Ⅲ)太郎が2個の玉を獲得した場合
題意を満たす取り出し方の場合の数について考える.
まず,色に関係なく太郎が2個の玉を獲得する場合の数は, 通り.
通り.
次に太郎が2個の玉を獲得し,かつその2個の玉に赤玉がない場合の数は, 通り.
通り.
よって,太郎が2個の玉を獲得し,かつその中に少なくとも1個の赤玉が含まれている場合の数は, 通り.
通り.
以上,(Ⅰ)~(Ⅲ)より,題意を満たす場合の数は, 通り.
通り.
よって,求める確率は,
 ……(答)
……(答)(ⅲ)
〇太郎が2回とも同色の玉を取り出す確率((56)~(59)について)
2回目に太郎が取り出しを行うと,太郎,花子合わせて3回取り出しを行ったことになる.この3回の玉の取り出し方の総数は 通り.
通り.
(Ⅰ)太郎が2回とも赤玉を取り出す場合の数
花子が赤玉を取り出さない場合,花子の取り出し方は7通りあるため, 通り.
通り.
花子が赤玉を取り出す場合, 通り.
通り.
 通り.
通り.
(Ⅱ)太郎が2回とも青玉を取り出す場合の数
花子が青玉を取り出さない場合,花子の取り出し方は8通りあるため, 通り.
通り.
花子が青玉を取り出す場合, 通り.
通り.
 通り.
通り.
(Ⅲ)太郎が2回とも白玉を取り出す場合の数
花子が白玉を取り出さない場合,花子の取り出し方は9通りあるため, 通り.
通り.
花子が白玉を取り出す場合, 通り.
通り.
 通り.
通り.
以上,(Ⅰ)~(Ⅲ)より,題意を満たす場合の数は, 通り.
通り.
よって,求める確率は, ……(答)
……(答)〇花子が2回のゲームを通じて獲得した玉に書かれた数の和が15となる確率((60)~(63)について)
2回のゲームにおける玉の取り出し方の総数は, 通り.
通り.
題意を満たすには花子は4個の玉を獲得せねばならない.なぜなら,3個の玉の数の和が最大となるのは3個の玉に書かれた数字が5,4,4のときであるが,和を計算すると13となり,15には届かないからである.
4個の玉を獲得し,かつ4個の玉に書かれた数の和が15となるには,玉に書かれた数の組み合わせが の2パターンに限られる.
の2パターンに限られる.
(Ⅰ)玉に書かれた数の組み合わせが の場合
の場合
花子が4個の玉を獲得する取り出し方は,4,5,2,4か2,4,4,5の順番で玉が取り出されたとき.
 通り.
通り.
(Ⅱ)玉に書かれた数の組み合わせが の場合
の場合
花子が4個の玉を獲得する取り出し方は,3,4,3,5か3,5,3,4の順番で玉が取り出されたとき.
 通り.
通り.
以上,(Ⅰ)と(Ⅱ)より,題意を満たす取り出し方の総数は 通り.
通り.
よって,求める確率は, ……(答)
……(答)






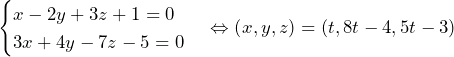
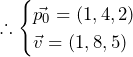 ……(答)
……(答)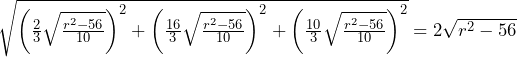
![Rendered by QuickLaTeX.com \int_{x_m}^{x_a+1}\left|m\left(x\right)-a\left(x\right)\right|dx=\int_{4}^{7}\left|x^2-8x+17-\left(\frac{1}{3}x^2-4x+17\right)\right|dx=\int_{4}^{7}\left|\frac{2}{3}x\left(x-6\right)\right|dx=\int_{4}^{6}\left\{-\frac{2}{3}x\left(x-6\right)\right\}dx+\int_{6}^{7}{\frac{2}{3}x\left(x-6\right)}dx=\left[2x^2-\frac{2}{9}x^3\right]_4^6+\left[\frac{2}{9}x^3-2x^2\right]_6^7=\frac{76}{9}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f16c686959dba9c1141ca1d2b264f9d3_l3.png) ……(答)
……(答) ……(答)
……(答)