2018年慶應義塾大学総合政策|数学過去問徹底研究 大問6 方針の立て方 (1) 解答欄の形式から,を用いてはいけないため,とについての等式を立てれば良いと分かる.この内,についての等式は,立てるまでもなく(座標)であるため,本解では省略した. (2) 特筆事項なし. (3) 実際にぐらいまで考えて
- …続きを読む
-
2018年慶應義塾大学総合政策|数学過去問徹底研究 大問6
方針の立て方
(1)
解答欄の形式から, を用いてはいけないため,
を用いてはいけないため, と
と についての等式を立てれば良いと分かる.この内,
についての等式を立てれば良いと分かる.この内, についての等式は,立てるまでもなく(
についての等式は,立てるまでもなく( 座標)
座標) であるため,本解では省略した.
であるため,本解では省略した.(2)
特筆事項なし.(3)
実際に ぐらいまで考えてみれば,解答が予測できる上に,何故そうなるのかの理由も分かる.
ぐらいまで考えてみれば,解答が予測できる上に,何故そうなるのかの理由も分かる.(4)
前問同様,最初の数回を具体的に考えれば解法を得られる.前問の試行で得られた知見を用いれば,比較的簡単に,期待値の評価ができる.解答例
(63)(64)……01
(65)(66)……02
(67)(68)……01
(69)(70)……00
(71)(72)……06
(73)(74)……02
(75)(76)……06
(77)(78)……06
(79)(80)……12解説
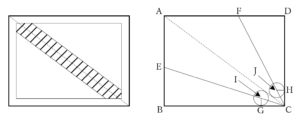
(1)
 座標は
座標は である.
である. 座標を
座標を とする.点と直線の距離の公式より,直線PR(
とする.点と直線の距離の公式より,直線PR( )と点
)と点 との距離について,
との距離について,

となる.点 は,直線PRよりも下側にあるため,
は,直線PRよりも下側にあるため, である.
である.

 ……(答)
……(答)(2)
 となる.
となる.
 ……(答)
……(答)(3)
 となる.
となる.
第3ラウンド以降は は
は か
か のどちらかとなる.
のどちらかとなる.
 となる確率について考えると,第3ラウンド以降の14回の対戦全てが「R対Rが2組,S対Sが1組」という当たり方をせねばならない.これが起こる確率は,
となる確率について考えると,第3ラウンド以降の14回の対戦全てが「R対Rが2組,S対Sが1組」という当たり方をせねばならない.これが起こる確率は, である.よって,
である.よって, となる確率は
となる確率は となり,明らかに,
となり,明らかに, となる確率の方が大きい.
となる確率の方が大きい.
よって,求める座標は から求められる点で,
から求められる点で, ……(答)
……(答)(4)
第1ラウンドが,
(ⅰ)R対P,R対S,R対Sの場合(場合の数は6通り)
→ →
→ となる.
となる.
(ⅱ)R対P,R対R,S対Sの場合(場合の数は3通り)
→ →
→ となる.
となる.
(ⅲ)S対P,R対R,R対Sの場合(場合の数は6通り)
→ →
→ となる.
となる.
よって, となる.
となる.
 (12)……(答)
(12)……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。








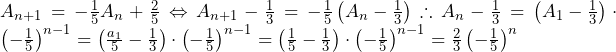
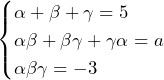
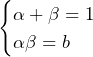
 ……(答)
……(答)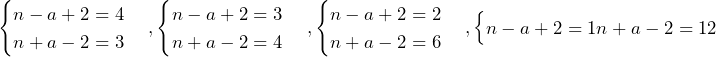
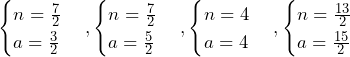
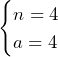 のみ.これより,答えは,
のみ.これより,答えは,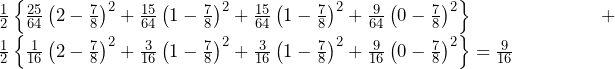 ……(答)
……(答)