4技能入試に向けて外部試験導入が進んでいる昨今、大学入試において英検準1級を取得するメリットは非常に大きいです。 2級に比べるとやや難しくなりますが受験勉強の範疇で十分対応が可能で、TOEICなどの他の外部試験と比べると比較的安価で対策もしやすいのでおすすめの資格と言えるでしょう。 実際の過去問は
- …続きを読む
- 4技能入試に向けて外部試験導入が進んでいる昨今、大学入試において英検準1級を取得するメリットは非常に大きいです。
[toc]
2級に比べるとやや難しくなりますが受験勉強の範疇で十分対応が可能で、TOEICなどの他の外部試験と比べると比較的安価で対策もしやすいのでおすすめの資格と言えるでしょう。
実際の過去問は公式サイトで最新3回分が無料で公開されています。
マイナーチェンジされることもありますが、大枠はほとんど変わりませんので最新の問題(2018年第1回)をもとに傾向と対策をみていきましょう。まず試験全体の話ですが、現在はリーディング・リスニング・ライティングの問題を解く1次試験と試験官と対面で英語を話す2次試験に分かれています。
将来的に1日で試験を行うようになる可能性はありますが、しばらくは現行の試験形態のままで行われるでしょう。
まずは筆記試験について対策をお伝えしていきます。
筆記試験問題形式
Reading 90分
第1問 語彙25問、第2問 長文穴埋め2題、第3問 長文3題、第4問 英作文(120-150words)
Listening 約30分
Part1 Dialogues、Part2 Passages、Part3 Real-Life
リーディングセクションについて
日本の既存の教育を受けている人であれば、一番得意となりうるセクションです。
大学受験で行っている長文対策で対応できる部分もありますが、できない部分もあります。下記でどのように対策を行ったら良いのかを記載していきます。第1問 語彙
単に準1級に受かるだけであればこのセクションで高得点を取る必要はありません。
ただし準1級の長文パートは2級よりも語彙力を要求されますので最低限の準備はしておく必要があります。具体的には単語王レベルの語彙は絶対に必要です。
何はともあれまずは単語王をしっかり終わらせましょう。
いきなり英検準1級用の単語帳に手を出しても良いのですが、単語王レベルで不安が残る状態だとスムーズにいかない場合があるのでまずは今使用している単語帳(単語王でなくてもよい)を仕上げるのがよいでしょう。第2問 長文穴埋め
長文とは言っても3段落程度の短い文章ですので語数は多くありません。
内容も平易で問題も答えやすいものばかりとなっています。早慶レベルの問題と比べればはるかに解きやすく早慶を狙う受験生であれば満点を狙ってほしいセクションです。
ここでの失点が目立つようであれば一度2級レベルの問題に戻るといいでしょう。第3問 長文
標準的な長文問題を3題解くことになります。
内訳としては3パラグラフの文章が2題と4パラグラフの文章が1題で設問数はパラグラフ数と同一となっています。つまり、基本的には1つのパラグラフに1つの問題が対応しているわけです。
問題を解くうえでは1つのパラグラフを読み終わったらそれに対応した問題を解くと読み返し無しでスムーズに解けるでしょう。
選択肢に意地悪なものがほとんどないので、普段の受験勉強の延長として過去問に取り組むだけで十分な対策になります。さらにリーディングの具体的な対策、勉強法、合格点、目標点についてはこちらでも解説しています。
英検準1級リーディング対策!早稲田入試でも利用できるその攻略法とは
ライティングセクション
英検準1級の英作文では120〜150語程度の英作文が1題課されます。
話題は社会的なものが多いですが、ヒントとして4つのポイントが提示されておりその中から2つを選んで書くことになります。
理由づけは基本的にそのポイントに従ってやればよく、問題形式は毎回変わらないのでテンプレートを作成して覚えておけば語数に対してやることは意外と少ないです。さらにライティングの具体的な対策、勉強法、合格点、目標点についてはこちらでも解説しています。
英検準1級ライティング対策!早稲田入試でも利用できるその攻略法とは
リスニングセクションについて
英検に限らずこうしたリスニングの試験で得点を伸ばす一番の方法は先読みです。
先読みとは放送前に選択肢に目を通しておくことを言います。
特に英検は時間に余裕のある試験ですので、
合格レベルの学力があれば必ず時間は余ります。順調にいけば10分程度余って見直しに2~3分、
残りの7~8分を先読みの時間に当てることができます。余裕があれば余白に何を聞かれそうかメモしておいてもいいでしょう。
ただ筆記で予想外に苦戦するということも十分考えられますので、
その場合は最低限Part3のSituationとQuestionだけでも目を通しましょう。
というのもこのパートはSituationが文章で説明されているのでpart1とpart2に比べて目を通すのに時間がかかるからです。また特にPart1については放送が始まる前に長めの指示(基本的に毎回同じ内容)が流れるのでその時間中にも先読みを行うことができます。
先読みをやるかどうかで取り組みやすさが段違いに変わりますのでこれは必ず行うようにしてください。ただし多少慣れが必要な部分もあるので、過去問に取り組む際は時間を測ってフルセットで行い、自分がどれくらい先読みの時間を確保できるのかをしっかり把握しておきましょう。
また言うまでもないですが、解けなかった問題に執着するのは絶対にやめましょう。
マークを終えたら意識を切り替えて次の問題に取り組むのが大事です。さらにリスニングの具体的な対策、勉強法、合格点、目標点についてはこちらでも解説しています。
英検準1級リスニング対策!早稲田入試でも利用できるその攻略法とは
スピーキングセクションについて
毎回1次試験合格者の約8割以上は2次試験合格を果たしています。
ですが、それは1次試験の対策をしっかりしている人であれば、2次試験の対策もしっかり行っているからうかるわけであっても、何も対策をせずうかるということはありえません。
試験当日は、自信を持って答えられるように準備を怠らずに勉強をしてください。実際の問題構成は以下の通りです。
入室&挨拶+スモールトーク
↓
イラストのナレーション 1題(準備時間1分)
↓
イラストに関する質問2題(2問目はカードを伏せる)
↓
社会的な質問2題
英検の公式サイトのサンプル問題では、受動喫煙問題・日本の犯罪率・政府の決定に対する世論の役割が出題されています。こうしたテーマを対して準備なしで語るのは一見難しいように思えるかもしれません。
しかし、これらのテーマは多くが英作文の対策をしっかりやっていれば問題なく応答できます。
もちろん淀みなくスラスラ喋るということになれば難しいでしょうが、多少言い淀んでも大きく減点されることはありません。相手の質問を聞いて少し考え、ポイントを外さず応答する。それで十分です。質問が聞き取れなかったら素直に聞き返しましょう。
流暢さももちろん重要ですが、
面接レベルの内容の会話で一度だけで完璧に聞き取って、完璧な答えを返すということは少ないです。質問の意図を正確に理解して、答えることの方がはるかに重要です。対策としては英作文で勉強したテーマを口頭である程度話せるようにするだけで大丈夫です。具体的には添削済みの自分の答案を音読するといいでしょう。
発音等まで気をつけたい場合は音読のときに録音してみると自分の発音の良し悪しがわかるのでおすすめです。当塾ではネイティブの講師や英語圏に在住経験のあるハイレベルの講師を採用して、何をどうしたら良いのかという点まで対策をしております。
英検準一級対策でご不明な点があればお気軽にご連絡ください。これからの入試において、何をどうしたらよいのか、ご相談レベルの話でもご不安がある場合は一度ご相談をいただければと思います。こちらからご相談ください。







![Rendered by QuickLaTeX.com \int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left(q-x^2\right)dx=\int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left\{\left(r+\frac{1}{2}\right)^2-x^2\right\}dx=\left[\left(r+\frac{1}{2}\right)^2x-\frac{1}{3}x^3\right]_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}=\frac{4}{3}r^3+2r^2+r+\frac{1}{6}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-94aeca5089102bd3c6cc95fc6a86c7e9_l3.png) ……(答)
……(答)
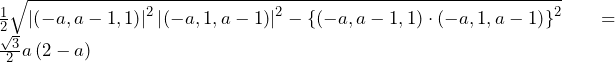
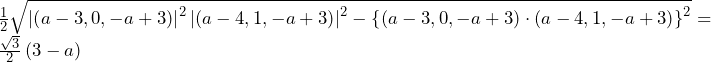
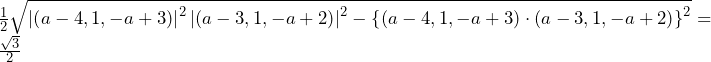
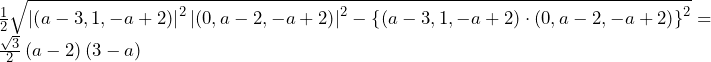
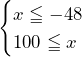 となってしまい,なぜ不適かが分かり,解法が思いつくだろう.
となってしまい,なぜ不適かが分かり,解法が思いつくだろう.
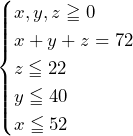
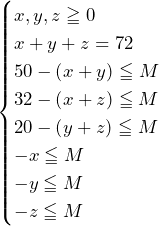
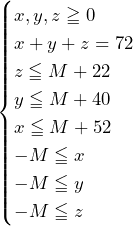
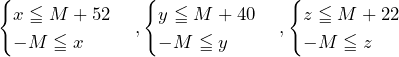
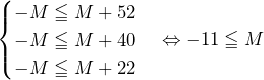
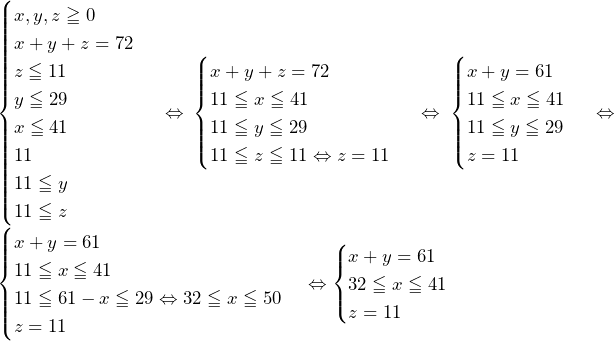
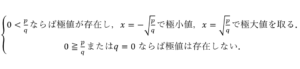
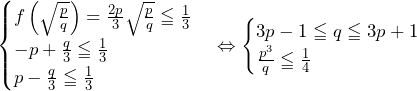
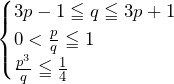 ……(答)
……(答)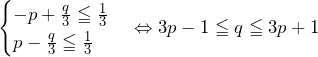
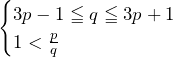 ……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.
……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.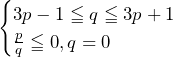 ……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.
……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.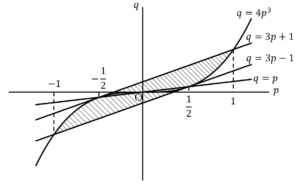
![Rendered by QuickLaTeX.com 2\left[\int_{0}^{\frac{1}{2}}\left\{3p+1-\left(3p-1\right)\right\}dp+\int_{\frac{1}{2}}^{1}\left(3p+1-4p^3\right)dp\right]=2\left\{\left[2p\right]_0^{\frac{1}{2}}+\left[-p^4+\frac{3}{2}p^2+p\right]_{\frac{1}{2}}^1\right\}=\frac{27}{8}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f56368e0ec425cd83fbebcfd5460687d_l3.png) ……(答)
……(答)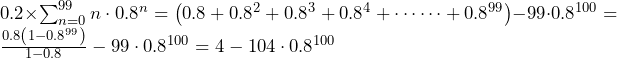
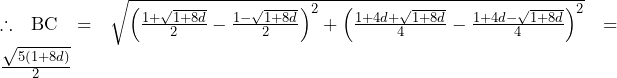
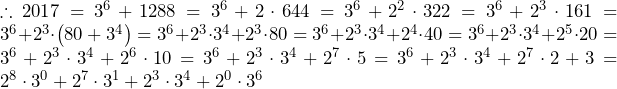 ……(答)
……(答)