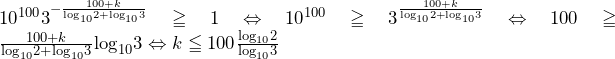方針の立て方 (1) ガウス記号に関する重要な性質:を使うだけ.ガウス記号は文系数学頻出のテーマのため,この重要な性質とともに覚えておこう. (2) 前問を一般化したもの(前問は本問ののパターンである)であることに気付きたい.入試数学では,まず具体的なパターンでやらせ,その次の問題で一般化するという
- …続きを読む
-
方針の立て方
(1)
ガウス記号に関する重要な性質:![Rendered by QuickLaTeX.com \left[x\right]=n\Leftrightarrow n\leqq x<n+1](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMcAAAATAQAAAAAM0SRSAAAAAnRSTlMAAHaTzTgAAAANSURBVBgZYxgFIwgAAAHuAAGiSxnBAAAAAElFTkSuQmCC) を使うだけ.ガウス記号は文系数学頻出のテーマのため,この重要な性質とともに覚えておこう.
を使うだけ.ガウス記号は文系数学頻出のテーマのため,この重要な性質とともに覚えておこう.(2)
前問を一般化したもの(前問は本問の のパターンである)であることに気付きたい.入試数学では,まず具体的なパターンでやらせ,その次の問題で一般化するという出題形式が多い.一般化されると途端に難しくなったと感じがちだが,前問と同じように処理していけばよい.つまり,
のパターンである)であることに気付きたい.入試数学では,まず具体的なパターンでやらせ,その次の問題で一般化するという出題形式が多い.一般化されると途端に難しくなったと感じがちだが,前問と同じように処理していけばよい.つまり,![Rendered by QuickLaTeX.com \left[x\right]=n\Leftrightarrow n\leqq x<n+1](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMcAAAATAQAAAAAM0SRSAAAAAnRSTlMAAHaTzTgAAAANSURBVBgZYxgFIwgAAAHuAAGiSxnBAAAAAElFTkSuQmCC) を使って変形し,その範囲で
を使って変形し,その範囲で の倍数である
の倍数である を拾い上げていけばよい.ただし,前問では
を拾い上げていけばよい.ただし,前問では に制限がないが,本問では制限がついてしまっていることに注意.
に制限がないが,本問では制限がついてしまっていることに注意.(3)
前問の議論で, と
と と
と と
と で場合分けしたので,本問でもこれと同様に場合分けして考えればよい.
で場合分けしたので,本問でもこれと同様に場合分けして考えればよい.解答例
(1)
![Rendered by QuickLaTeX.com \left[\sqrt[3]{n}\right]=2\Leftrightarrow2\leqq\sqrt[3]{n}<3\Leftrightarrow2^3\leqq n<3^3\Leftrightarrow8\leqq n<27](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAboAAAAWAQAAAACeJWQJAAAAAnRSTlMAAHaTzTgAAAARSURBVBgZYxgFo2AUjIJhDQAE5gABhP15QQAAAABJRU5ErkJggg==)
である.この範囲で4の倍数となるものが答えである.
 ……(答)
……(答)(2)
 の値に制限がない場合,
の値に制限がない場合,
![Rendered by QuickLaTeX.com \left[\sqrt[3]{n}\right]=p_n\Leftrightarrow p_n\leqq\sqrt[3]{n}<p_n+1\Leftrightarrow{p_n}^3\leqq n<\left(p_n+1\right)^3\Leftrightarrow{p_n}^3\leqq n<{p_n}^3+3{p_n}^2+3p_n+1](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAAuAQAAAABbyLOCAAAAAnRSTlMAAHaTzTgAAAAaSURBVEjH7cGBAAAAAMOg+VNf4AhVAQAAwDMOMgABrmQ1DgAAAABJRU5ErkJggg==)
となる.この範囲に, の倍数である
の倍数である は,
は,

の 個ある.ここで,
個ある.ここで, は,
は, を満たす最大の自然数である.つまり,
を満たす最大の自然数である.つまり, ならば
ならば ならば
ならば ならば
ならば である.
である.
今は という制限があるが,
という制限があるが, までは上記の議論が使える.
までは上記の議論が使える.
さて, より
より![Rendered by QuickLaTeX.com p_n\leqq\left[\sqrt[3]{{10}^6}\right]=\left[100\right]=100](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAN4AAAAiAQAAAAAYTFp4AAAAAnRSTlMAAHaTzTgAAAAQSURBVBgZYxgFo2AUDEMAAAPaAAGkujW3AAAAAElFTkSuQmCC) であるから,
であるから, のときを別個で考えれば必要十分.
のときを別個で考えれば必要十分.
 となる
となる は
は のみであるから,
のみであるから, の倍数である
の倍数である は
は の1個のみ.
の1個のみ.
よって,求める個数は,
 個……(答)
個……(答)(3)
前問の議論より,
(Ⅰ) のとき
のとき
 の倍数である
の倍数である は,
は,

である.これらを で割った余りは,順番に
で割った余りは,順番に である.
である.
(Ⅱ) のとき
のとき
 の倍数である
の倍数である は,
は,

である.これらを で割った余りは,順番に
で割った余りは,順番に である.
である.
(Ⅲ) のとき
のとき
 の倍数である
の倍数である は,
は,

である.これらを で割った余りは,順番に
で割った余りは,順番に である.
である.
(Ⅳ) のとき
のとき
 の倍数である
の倍数である は,
は,

である.これらを で割った余りは,順番に
で割った余りは,順番に である.
である.
(Ⅴ) のとき
のとき
 の倍数である
の倍数である は,
は,

である.これを で割った余りは,100である.
で割った余りは,100である.
以上,(Ⅰ)~(Ⅴ)より,
 ……(答)
……(答)







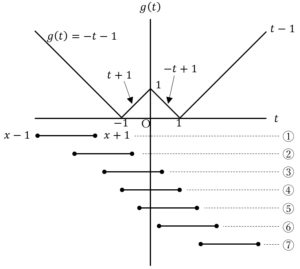
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{-1}\left(-t-1\right)dt+\frac{1}{2}\int_{-1}^{x+1}\left(t+1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{-1}+\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^{x+1}=\frac{1}{2}\left(x^2+2x+2\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-39f866a3cf0aa6d994ba926375844cd8_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{-1}\left(-t-1\right)dt+\frac{1}{2}\int_{-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{x+1}\left(-t+1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{-1}+\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^{x+1}=\frac{1}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-6432dfc95b1fd3fc8ab0566581f9478a_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{1}\left(-t+1\right)dt+\frac{1}{2}\int_{1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{x-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^1+\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_1^{x+1}=\frac{1}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-b5cfbd01a7849bbc24254319f21aa456_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{1}\left(-t+1\right)dt+\frac{1}{2}\int_{1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_{x-1}^1+\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_1^{x+1}=\frac{1}{2}\left(x^2-2x+2\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-02980b127b2365339e8eef20ba5c599a_l3.png)
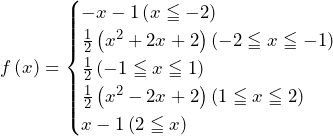
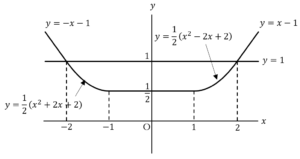
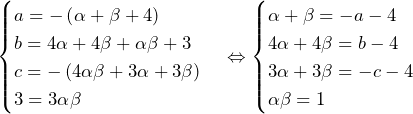
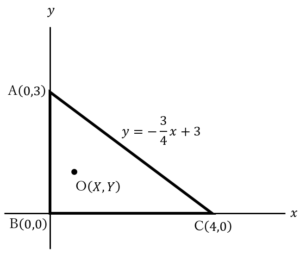
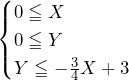 ……(*)
……(*)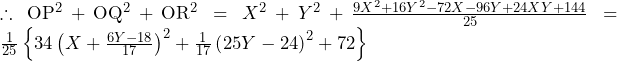
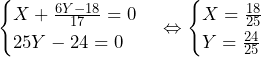 で
で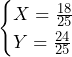 は(*)を満たす.
は(*)を満たす.