方針の立て方 どれも基本問題であり,特筆事項なし. 解答例 真数条件より,が必要. (1) 2次方程式の実数解が存在しないためには,判別式が負であれば必要十分. これは真数条件を満たす. ……(答) (2) 2次方程式の実数解がただ1つ存在するためには,判別式が0であれば必要十分. このもとで,2次
- …続きを読む
-
方針の立て方
どれも基本問題であり,特筆事項なし.
解答例
真数条件より,
 が必要.
が必要.
(1)
2次方程式の実数解が存在しないためには,判別式が負であれば必要十分.
![Rendered by QuickLaTeX.com \therefore\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}<0\Leftrightarrow\left({\mathrm{log}}_2{t}\right)^2\left\{\left({\mathrm{log}}_2{t}\right)^2-4\right\}<0\Leftrightarrow \begin{cases} {\mathrm{log}}_2{t}\neq0 \\ \left({\mathrm{log}}_2{t}\right)^2-4<0 \end{cases}\Leftrightarrow\begin{cases} t\neq1 \\ \frac{1}{4}<t<4 \end{cases}\Leftrightarrow\frac{1}{4}<t<1,1<t<4](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-8e0527003541c856f39f9c25a8c98acf_l3.png)
これは真数条件を満たす.
 ……(答)
……(答)(2)
2次方程式の実数解がただ1つ存在するためには,判別式が0であれば必要十分.
![Rendered by QuickLaTeX.com \therefore\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}=0\Leftrightarrow\left({\mathrm{log}}_2{t}\right)^2\left\{\left({\mathrm{log}}_2{t}\right)^2-4\right\}=0\Leftrightarrow{\mathrm{log}}_2{t}=0,\left({\mathrm{log}}_2{t}\right)^2-4=0\Leftrightarrow t=\frac{1}{4},1,4](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAABAAQAAAABpNt2oAAAAAnRSTlMAAHaTzTgAAAAcSURBVFjD7cExAQAAAMKg9U9tDQ+gAAAAAIBXAxPAAAFi5NraAAAAAElFTkSuQmCC)
このもとで,2次方程式の解は,

これより, の最小値は
の最小値は で,最大値は
で,最大値は でとる.
でとる.
よって, の最小値は
の最小値は ,最大値は
,最大値は ……(答)
……(答)(3)

よって,2次方程式は2つの相異なる実数解をもち,その解は,
![Rendered by QuickLaTeX.com x=\left({\mathrm{log}}_2{t}\right)^2+1\pm\sqrt{\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}}=\left({\mathrm{log}}_2{t}\right)^2+1\pm\log_2{t}\sqrt{\left({\mathrm{log}}_2{t}\right)^2-4}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAABSAQAAAAAnKH44AAAAAnRSTlMAAHaTzTgAAAAdSURBVFjD7cGBAAAAAMOg+VOf4AZVAQAAAAAA8A0ZTgAB+5IcFwAAAABJRU5ErkJggg==)

ここで と置き換えると,
と置き換えると,
 (
( )
)

 となるのは,
となるのは,

両辺を2乗して計算すると となり不適.つまり
となり不適.つまり












よって,最小値は
 のときで,
のときで, ……(答)
……(答)







![Rendered by QuickLaTeX.com \therefore\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}=0\Leftrightarrow\left({\mathrm{log}}_2{t}\right)^2\left\{\left({\mathrm{log}}_2{t}\right)^2-4\right\}=0\Leftrightarrow{\mathrm{log}}_2{t}=0,\left({\mathrm{log}}_2{t}\right)^2-4=0\Leftrightarrow t=\frac{1}{4},1,4](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a1e1073ddd84432fcb4f616a108cf763_l3.png)
![Rendered by QuickLaTeX.com x=\left({\mathrm{log}}_2{t}\right)^2+1\pm\sqrt{\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}}=\left({\mathrm{log}}_2{t}\right)^2+1\pm\log_2{t}\sqrt{\left({\mathrm{log}}_2{t}\right)^2-4}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-200c81e8a0ef4ddb7ff42a6bac0604ed_l3.png)
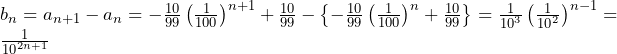
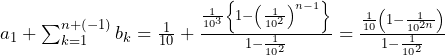
![Rendered by QuickLaTeX.com S_n=\sum_{k=1}^{n}\left\{\frac{1}{{10}^{2k}}\cdot{10}^{2k+1}\left(\frac{1}{a_k}-\frac{1}{a_{k+1}}\right)\right\}=10\sum_{k=1}^{n}\left(\frac{1}{a_k}-\frac{1}{a_{k+1}}\right)=10\left\{\left(\frac{1}{a_1}-\frac{1}{a_2}\right)+\left(\frac{1}{a_2}-\frac{1}{a_2}\right)+\cdots\cdots+\left(\frac{1}{a_n}-\frac{1}{a_{n+1}}\right)\right\}=10\left(\frac{1}{a_1}-\frac{1}{a_{n+1}}\right)=10\left[10-\frac{1-\frac{1}{{10}^2}}{\frac{1}{10}\left\{1-\frac{1}{{10}^{2\left(n+1\right)}}\right\}}\right]=\frac{1-\frac{1}{{10}^{2n}}}{1-\frac{1}{{10}^{2n+2}}}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a4bd52877826782c69edb6098ac4819d_l3.png)
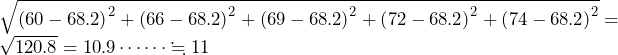 ……(答)
……(答)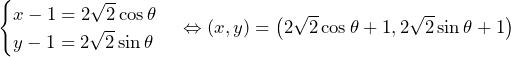 とおくことができる(
とおくことができる(![Rendered by QuickLaTeX.com A=\int_{0}^{2}f\left(t\right)dt=\int_{0}^{2}\left(\frac{3}{a}t^2-\frac{1}{a}t+A^2\right)dt=\left[\frac{1}{a}t^3-\frac{1}{2a}t^2+A^2t\right]_0^2=2A^2+\frac{6}{a}\Leftrightarrow2A^2-A+\frac{6}{a}=0](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-ab0bf548b4a46975e7979ac67d04290f_l3.png)
![Rendered by QuickLaTeX.com \int_{0}^{b}\left\{f\left(x\right)-f\left(b\right)\right\}dx=\int_{0}^{b}\left\{\frac{3}{a}x^2-\frac{1}{a}x-\frac{3}{a}b^2+\frac{1}{a}b\right\}dx=\left[\frac{1}{a}x^3-\frac{1}{2a}x^2-\frac{3}{a}b^2x+\frac{1}{a}bx\right]_0^b=-\frac{b^2\left(4b-1\right)}{2a}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a1ae218f005a4a94ff3accbf2e2f76ee_l3.png)
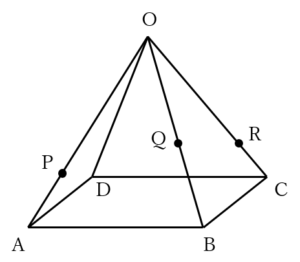
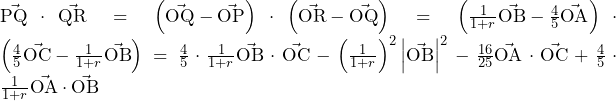
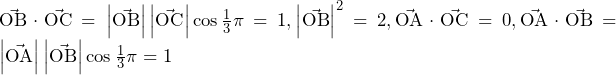 であるから,
であるから,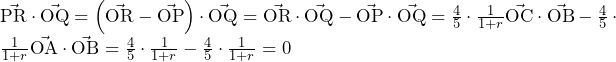 ……(答)
……(答)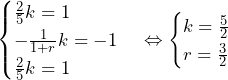
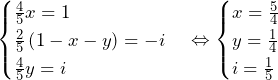
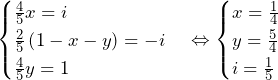
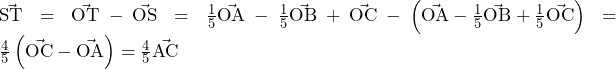
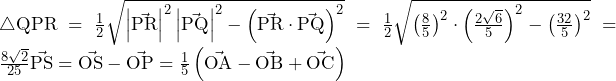 より,
より,