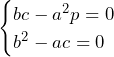2016年早稲田大学理工|過去問徹底研究 大問3 方針の立て方 (1) がもっと具体的に書き下せることから具体的に書き下してみる.するとの与えられ方が数列の漸化式と同じ形式であることが見抜けて解法が得られる. (2) という重要な性質から考える.(※極限値が分かっていてその証明をしたい場合にはを利用
- …続きを読む
-
2016年早稲田大学理工|過去問徹底研究 大問3
方針の立て方
(1)
 がもっと具体的に書き下せることから具体的に書き下してみる.すると
がもっと具体的に書き下せることから具体的に書き下してみる.すると の与えられ方が数列の漸化式と同じ形式であることが見抜けて解法が得られる.
の与えられ方が数列の漸化式と同じ形式であることが見抜けて解法が得られる.(2)
 という重要な性質から考える.(※極限値が分かっていてその証明をしたい場合には
という重要な性質から考える.(※極限値が分かっていてその証明をしたい場合には を利用する方が証明がしやすいことも併せておさえておこう.)
を利用する方が証明がしやすいことも併せておさえておこう.)(3)
複素数の円の問題であることと, の形を作り出したいというところから,
の形を作り出したいというところから, を考えることが思いつく.
を考えることが思いつく.解答例
(1)


 ……(答)
……(答)(2)
 より,
より,


 ……(答)
……(答)(3)

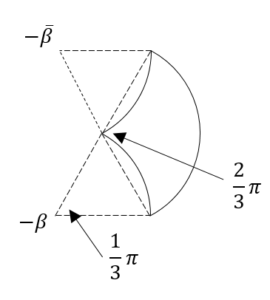
よって, を中心とする半径
を中心とする半径 の円……(答)
の円……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。






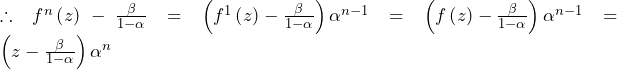


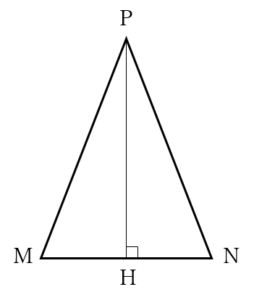
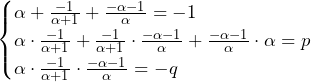
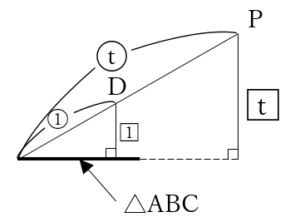
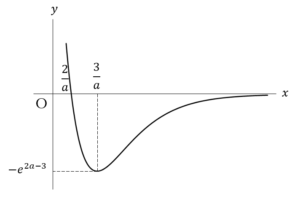 (上図が答え)
(上図が答え)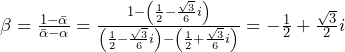 ……(答)
……(答)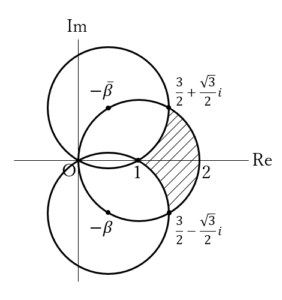
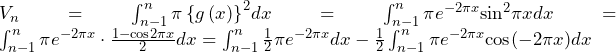
![Rendered by QuickLaTeX.com \int_{n-1}^{n}{\pi e^{-2\pi x}\cos{\left(-2\pi x\right)}}dx=-\frac{1}{2}\int_{-2\left(n-1\right)\pi}^{-2n\pi}{e^y\cos{y}}dy\bigm=-\frac{1}{2}\left[\frac{1}{2}e^y\left(\cos{y}+\sin{y}\right)\right]_{-2\left(n-1\right)\pi}^{-2n\pi}\bigm=-\frac{1}{4}\left(e^{-2n\pi}-e^{-2\left(n-1\right)\pi}\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-df13329429bcde4e2ecc7f39a38e588b_l3.png)
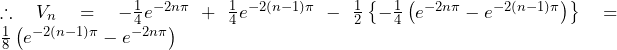 ……(答)
……(答)