方針の立て方 (1) どれも典型問題であるため特筆事項なし. (2) (マ)については,曲線の長さを公式を使って表した後に,極座標に置換すればよい. (ミ)についても,素直に計算をし,素直に等式を立てれば解答が得られる. (ム)について.対称性があるため,上半分だけを求めればよいことに気付くと計算が
- …続きを読む
-
方針の立て方
(1)
どれも典型問題であるため特筆事項なし.(2)
(マ)については,曲線の長さを公式 を使って表した後に,極座標に置換すればよい.
を使って表した後に,極座標に置換すればよい.
(ミ)についても,素直に計算をし,素直に等式を立てれば解答が得られる.
(ム)について.対称性があるため,上半分だけを求めればよいことに気付くと計算が楽になる.この問題に限らず,対称性に気付くことは重要である.そして,曲線の分かれ目となる点 の左側と右側で分けて面積を求めると考える.第1象限側は円弧であるため,面積の導出については特筆事項なし.左側については,最初は素直に
の左側と右側で分けて面積を求めると考える.第1象限側は円弧であるため,面積の導出については特筆事項なし.左側については,最初は素直に 座標で面積を定積分で表し,それを極座標変換する.極座標の問題で分からないときには一先ず
座標で面積を定積分で表し,それを極座標変換する.極座標の問題で分からないときには一先ず 座標で表し,それを極座標変換するという順序で解くと,何をやっているのかが分かりやすい.
座標で表し,それを極座標変換するという順序で解くと,何をやっているのかが分かりやすい.解答例
(1)
フ:
ヘ:
ホ:
(2)
マ:
ミ:
ム:
解説
(1)
〇半径(フについて)
 とおくと,
とおくと, と書ける.
と書ける.


両辺正のため,2乗しても同値性は崩れず,

よって,求める半径は ……(答)
……(答)〇点
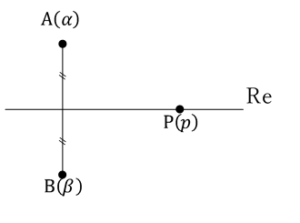
 の座標(ヘとホについて)
の座標(ヘとホについて)
点 の
の 座標を
座標を と置くと,接点の座標は
と置くと,接点の座標は となる.
となる.
よって,接線は,

これが点 を通るので,
を通るので,

よって,点 の座標は,
の座標は,
 ……(答)
……(答)(2)
〇最短経路の長さ(マについて)
曲線 の方程式を
の方程式を とすると,最短経路の長さは,
とすると,最短経路の長さは,

となる.ただし, は点
は点 の
の 座標であり,
座標であり, は点
は点 の
の 座標である.
座標である.
ここで,直角座標から極座標へ変換すると,

となり,


よって,最短経路の長さは, より,積分区間が入れ替わることに注意すれば,
より,積分区間が入れ替わることに注意すれば,

〇 (ミについて)
(ミについて)
(1)の結果を考えれば, であり,
であり, である.
である.
 より,
より, である.
である.
更に
![Rendered by QuickLaTeX.com \mathrm{AB}+\int_{\theta_0}^{\theta_1}\sqrt{\left\{f^\prime\left(\theta\right)\right\}^2+\left\{f\left(\theta\right)\right\}^2}d\theta=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}\sqrt{\left\{\alpha\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2+\left\{\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2}d\theta\bigm=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}{\sqrt{1+\alpha^2}\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}}d\theta=\frac{v}{\sqrt{v^2-1}}+\sqrt{1+\alpha^2}\beta\left[\frac{1}{\alpha}e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right]_{\frac{\pi}{2}}^{\theta_1}\bigm=\frac{v}{\sqrt{v^2-1}}-\frac{\beta}{\alpha}\sqrt{1+\alpha^2}+\frac{\beta}{\alpha}\sqrt{1+\alpha^2}e^{\alpha\left(\theta_1-\frac{\pi}{2}\right)}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAACiAQAAAAAyumchAAAAAnRSTlMAAHaTzTgAAAAjSURBVGje7cExAQAAAMKg9U9tDQ+gAAAAAAAAAAAAAAAA+DUx/gABwo5QDgAAAABJRU5ErkJggg==)
これと が等しくなるので,
が等しくなるので,
 ……(答)
……(答)
〇領域の面積(ムについて)
 のとき,
のとき, となる.
となる.
以下では,領域の上半分の面積を考える.最終的な答えはその2倍となる.
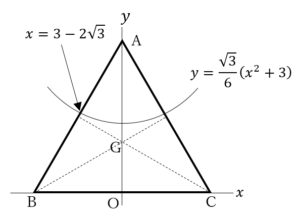
まず第1象限の図形について.これは(1)の議論から を満たす図形,つまり,中心
を満たす図形,つまり,中心 ,半径
,半径 の円の内部.中心を点
の円の内部.中心を点 とすると,
とすると, となる.よって,第1象限の図形の面積は,
となる.よって,第1象限の図形の面積は,

次に第2象限の図形について.
 であるから,
であるから, のとき,
のとき,
よって,第2象限の図形の面積は,

ここで,![Rendered by QuickLaTeX.com \int_{\pi}^{\frac{\pi}{2}}e^{2\theta-\pi}d\theta=\left[\frac{1}{2}e^{2\theta-\pi}\right]_\pi^{\frac{\pi}{2}}=\frac{1}{2}\left(1-e^\pi\right)](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAATAAAAAdAQAAAAAFxQ0CAAAAAnRSTlMAAHaTzTgAAAARSURBVBgZYxgFo2AUjALaAwAEawABJlMOYgAAAABJRU5ErkJggg==) であり,
であり,

であるから,
![Rendered by QuickLaTeX.com \int_{\pi}^{\frac{\pi}{2}}{e^{2\theta-\pi}\left(\sin{2\theta}+\cos{2\theta}\right)}d\theta=\int_{\pi}^{\frac{\pi}{2}}{\frac{1}{2}\left(e^{2\theta-\pi}\sin{2\theta}\right)^\prime}d\theta=\left[\frac{1}{2}e^{2\theta-\pi}\sin{2\theta}\right]_\pi^{\frac{\pi}{2}}=0](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAAtAQAAAADdXMEsAAAAAnRSTlMAAHaTzTgAAAAaSURBVEjH7cEBDQAAAMKg909tDwcUAAAAJwYN4wABO2sgJgAAAABJRU5ErkJggg==)

よって,上半分の面積は,

よって,求める面積は,
 ……(答)
……(答)







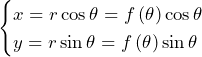
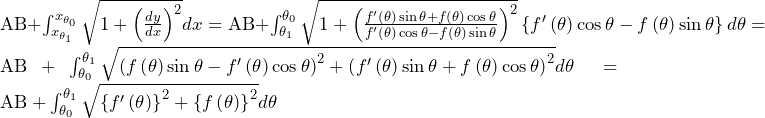
![Rendered by QuickLaTeX.com \mathrm{AB}+\int_{\theta_0}^{\theta_1}\sqrt{\left\{f^\prime\left(\theta\right)\right\}^2+\left\{f\left(\theta\right)\right\}^2}d\theta=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}\sqrt{\left\{\alpha\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2+\left\{\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2}d\theta\bigm=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}{\sqrt{1+\alpha^2}\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}}d\theta=\frac{v}{\sqrt{v^2-1}}+\sqrt{1+\alpha^2}\beta\left[\frac{1}{\alpha}e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right]_{\frac{\pi}{2}}^{\theta_1}\bigm=\frac{v}{\sqrt{v^2-1}}-\frac{\beta}{\alpha}\sqrt{1+\alpha^2}+\frac{\beta}{\alpha}\sqrt{1+\alpha^2}e^{\alpha\left(\theta_1-\frac{\pi}{2}\right)}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3251c46fb035b1c6f3d900fd751c1cf5_l3.png)
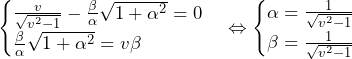 ……(答)
……(答)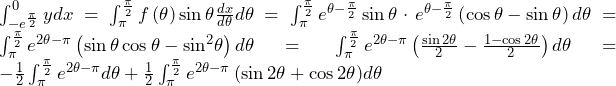
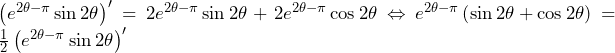
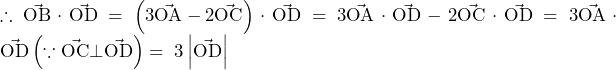 (
(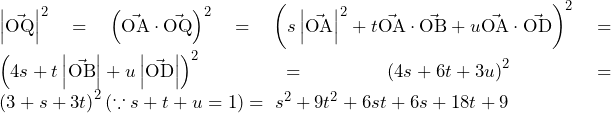
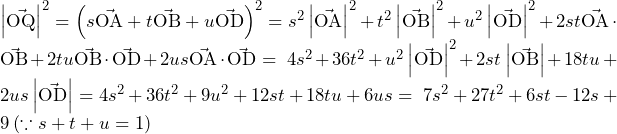
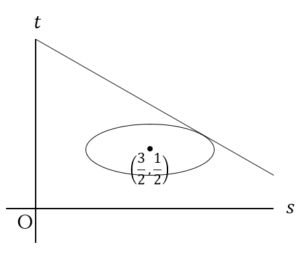
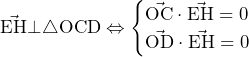
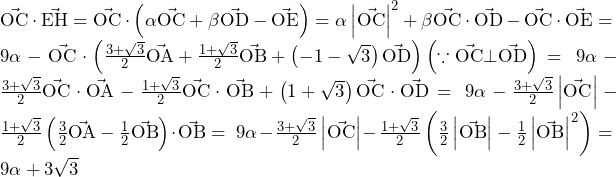
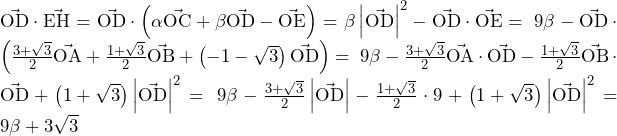
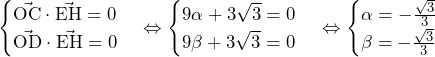
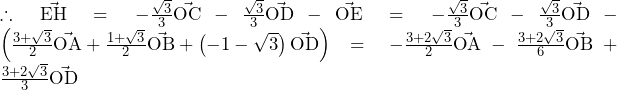
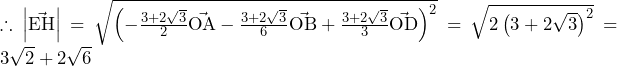

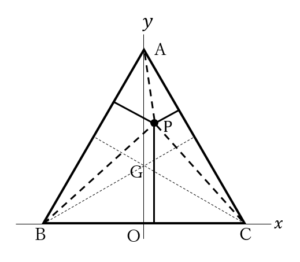
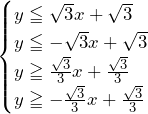
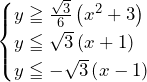
![Rendered by QuickLaTeX.com 2\int_{3-2\sqrt3}^{0}\left\{\left(\sqrt3x+\sqrt3\right)-\left(\frac{\sqrt3}{6}x^2+\frac{\sqrt3}{2}\right)\right\}dx=\left[-\frac{\sqrt3}{9}x^3+\sqrt3x^2+\sqrt3x\right]_{3-2\sqrt3}^0=16-9\sqrt3](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-ca7e2526c667d1ae7bb1ab5fab12914c_l3.png) ……(答)
……(答)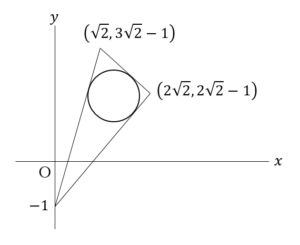
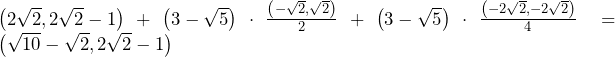 ……(答)
……(答)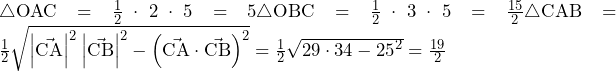 より,
より,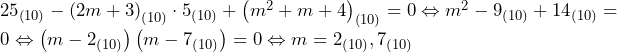
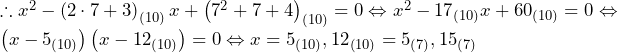
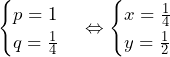 でとり,値を大きくするとある
でとり,値を大きくするとある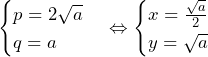 の両方でとり,それより
の両方でとり,それより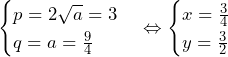 のとき,
のとき,


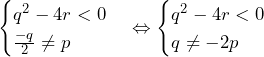 ……(答)
……(答)