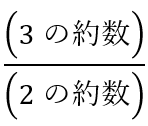
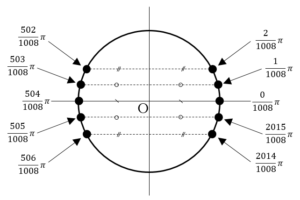
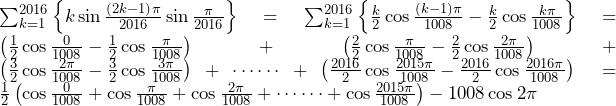方針の立て方 簡単にでも作図をすることで題意とつかめ,方針も得られる. (1) 基本問題であるため,特筆事項はない.角度に関する情報が何も問題文で与えられていないため,余弦定理を用いて角度の情報を得ることを考える. (2) 実際に作図することで,全ての三角形が合同であることが分かる.これを利用すると
- …続きを読む
- 方針の立て方
簡単にでも作図をすることで題意とつかめ,方針も得られる.
(1)
基本問題であるため,特筆事項はない.角度に関する情報が何も問題文で与えられていないため,余弦定理を用いて角度の情報を得ることを考える.
(2)
実際に作図することで,全ての三角形が合同であることが分かる.これを利用すると, に着目するのが有効だと分かる.後は余弦定理を用いればよいので,余弦定理に必要な
に着目するのが有効だと分かる.後は余弦定理を用いればよいので,余弦定理に必要な の情報を求める問題に帰着できる.(※
の情報を求める問題に帰着できる.(※ は二等辺三角形であるから,頂角の二等分線を引くことで求める解法も使える.)
は二等辺三角形であるから,頂角の二等分線を引くことで求める解法も使える.)
(3)
これも試しに まで作図してみると,本解答の図のように,ジグザグになっていることが分かる.
まで作図してみると,本解答の図のように,ジグザグになっていることが分かる.
解答例
(1)

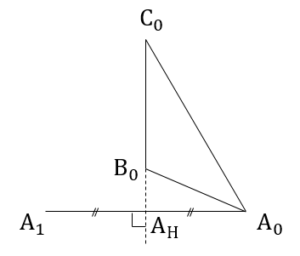
左図のように,線分 と直線
と直線 の交点を
の交点を する.すると,
する.すると,

である. に余弦定理を用いると,
に余弦定理を用いると,

であるから,

 ……(答)
……(答)(2)

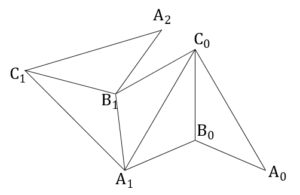
左図で全ての三角形は合同である.
よって, である.
である.
また, より,
より,

である.よって,

ここで, に正弦定理を用いると,
に正弦定理を用いると,


よって, に余弦定理を用いると,
に余弦定理を用いると,
 ……(答)
……(答)(3)
前問と同様に考えると,

上図のようになる.
 ……(答)
……(答)






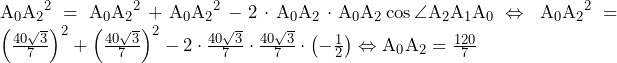 ……(答)
……(答)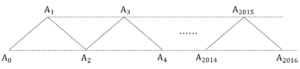
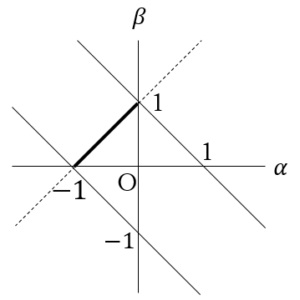
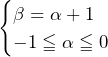
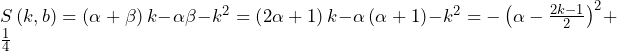
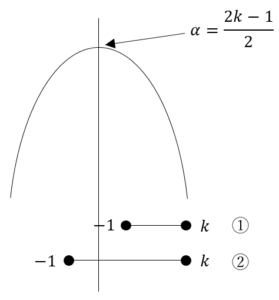
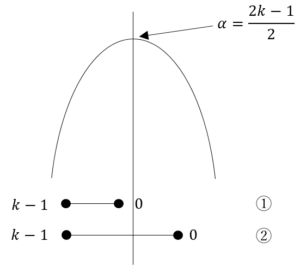
![Rendered by QuickLaTeX.com \int_{-1}^{-\frac{1}{2}}\left(-k^2-k\right)dk+\int_{-\frac{1}{2}}^{0}\frac{1}{4}dk+\int_{0}^{\frac{1}{2}}\frac{1}{4}dk+\int_{\frac{1}{2}}^{1}\left(-k^2+k\right)dk=\left[-\frac{1}{3}k^3-\frac{1}{2}k^2\right]_{-1}^{-\frac{1}{2}}+\left[\frac{1}{4}k\right]_{-\frac{1}{2}}^0+\left[\frac{1}{4}k\right]_0^{\frac{1}{2}}+\left[-\frac{1}{3}k^3+\frac{1}{2}k^2\right]_{\frac{1}{2}}^1=\frac{5}{12}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-e0c8bfe825912f02cafeb7f3d4b9999f_l3.png) ……(答)
……(答)