全体講評 難易度 ☆☆☆☆ 長文文字数1,446文字 出題傾向や全体としての分量などは昨年とほぼ変わりません。 本学部の英語は日本の全大学の中でもトップレベルの難易度となっており、多くの受験生にとって厳しい内容です。 特にpart1の文章は例年専門性が高く難解な内容のものが出題されており、今年も難解
- …続きを読む
-
全体講評
難易度 ☆☆☆☆ 長文文字数1,446文字
出題傾向や全体としての分量などは昨年とほぼ変わりません。
本学部の英語は日本の全大学の中でもトップレベルの難易度となっており、多くの受験生にとって厳しい内容です。特にpart1の文章は例年専門性が高く難解な内容のものが出題されており、今年も難解な内容でした。
確実に取れるところを見極めてひとつのところに時間を使いすぎないように気をつけましょう。意外と解きやすい問題も結構あるのでそうした問題に時間を使うのが大事になります。簡単な問題が時間がなくて解けないなどということがないようにしてください。PartⅠ
例年通り3つのパッセージを読んでいくタイプの長文読解問題でした。視覚認知と専門的能力の関係性についての内容でしたが、TextⅠが特に難易度が高かった印象です。
ただしTextⅡとTextⅢは比較的読みやすいものでしたので、そこで稼げていれば合格点は確保できるでしょう。
試験全体のタイムマネジメントを考えると、ここは他よりも時間を食いがちなセクションなので、先に他のセクションを解いてからやるようにするといいかもしれません。PartⅡ
例年通りの整序問題です。文章の内容は熱電発電の活用についての内容でしたが、昨年度と比して特に難易度が変化している印象はありません。
PartⅢ
例年と変わらずAが長文の空所補充問題、Bが文・段落整序問題でした。
今年度のA問題は音楽と人間の感情についての内容で、昨年度のブラックホールについての文章に比べるとかなり読みやすかったはずです。
問題は文法知識でほぼ解けるようになっているので、ここで取りこぼしが多いと他で稼がなくてはならなくなり、そのぶん合格が難しくなってしまいます。
Bに関しては2題しかないうえにそれなりに難易度が高いので、苦手な人は最後に回しても良いかもしれません。一番最悪なのは時間をかけた問題を間違えることなので、自分の得意不得意を見極めて問題を解く順番を事前に決めておきましょう。PartⅣ
このセクションは去年に比べてAの部分が形式としてやや変化しました。去年は一続きの文章であったのが、今年は短文問題に切り替わっています。ただし全体の難易度としてはそれほど変化は無く、引き続き本学部の問題の中では解きやすいセクションであることに変わりはありません。
PartⅤ
例年通り、英語の定義と例文から単語を特定する語彙問題でした。毎年それほど難しい単語は出題されませんが、解答形式に慣れていないと予想以上に時間を喰ってしまう可能性があります。スムーズに解答できるように過去問での練習は必須です。このセクションで確実に高得点を取りたいということであれば普段から英英辞書を使うようにしてみてください。慣れないうちは大変かもしれませんが、場合によっては英和辞書よりも単語のイメージが掴みやすい場合も多々あります。時間があるのであれば自身の使っている単語帳に載っている単語を英英で調べ直すと良いでしょう。おおよその目安として4000~5000語(共通試験や英検2級相当)レベルの語彙があれば普通に英英辞典を読むことができます。もちろんこれは別に一気にやることではないので1日10語など毎日コツコツやっていきましょう。語学の勉強はとにかく1日1日の積み重ねになりますので根気強く学習していってください。
2022年に早稲田理工に合格するためにすることは?参考書は?
早稲田理工に合格するためには、文法力とともに難解な文章を読み切るための長文読解力が必要になります。勉強法の詳細はこちらで紹介しています。
文法問題は基本的には桐原1000やヴィンテージ、アップグレードといった網羅系の問題集を一冊完璧にし終えた後で、整序問題を練習していきましょう。
[itemlink post_id="17957"]
整序問題は河合の500か門脇先生のをやっておくと良いでしょう。長文問題については、難易度が非常に高いです。普段から理系の長文を読み慣れていないと通常の英語長文問題集だと対処できません。Natureなどの理系論文を読んでいくと良いでしょう。
長文自体のテーマが他大学や市販の教材に出てくるような頻出テーマが出てくることは少なく、語彙レベルも高いので過去問を徹底的に研究することが合格への近道になります。















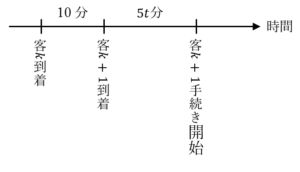
![Rendered by QuickLaTeX.com \therefore\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}<0\Leftrightarrow\left({\mathrm{log}}_2{t}\right)^2\left\{\left({\mathrm{log}}_2{t}\right)^2-4\right\}<0\Leftrightarrow \begin{cases} {\mathrm{log}}_2{t}\neq0 \\ \left({\mathrm{log}}_2{t}\right)^2-4<0 \end{cases}\Leftrightarrow\begin{cases} t\neq1 \\ \frac{1}{4}<t<4 \end{cases}\Leftrightarrow\frac{1}{4}<t<1,1<t<4](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-8e0527003541c856f39f9c25a8c98acf_l3.png)
![Rendered by QuickLaTeX.com \therefore\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}=0\Leftrightarrow\left({\mathrm{log}}_2{t}\right)^2\left\{\left({\mathrm{log}}_2{t}\right)^2-4\right\}=0\Leftrightarrow{\mathrm{log}}_2{t}=0,\left({\mathrm{log}}_2{t}\right)^2-4=0\Leftrightarrow t=\frac{1}{4},1,4](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a1e1073ddd84432fcb4f616a108cf763_l3.png)
![Rendered by QuickLaTeX.com x=\left({\mathrm{log}}_2{t}\right)^2+1\pm\sqrt{\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}}=\left({\mathrm{log}}_2{t}\right)^2+1\pm\log_2{t}\sqrt{\left({\mathrm{log}}_2{t}\right)^2-4}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-200c81e8a0ef4ddb7ff42a6bac0604ed_l3.png)
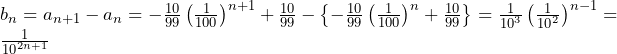
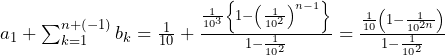
![Rendered by QuickLaTeX.com S_n=\sum_{k=1}^{n}\left\{\frac{1}{{10}^{2k}}\cdot{10}^{2k+1}\left(\frac{1}{a_k}-\frac{1}{a_{k+1}}\right)\right\}=10\sum_{k=1}^{n}\left(\frac{1}{a_k}-\frac{1}{a_{k+1}}\right)=10\left\{\left(\frac{1}{a_1}-\frac{1}{a_2}\right)+\left(\frac{1}{a_2}-\frac{1}{a_2}\right)+\cdots\cdots+\left(\frac{1}{a_n}-\frac{1}{a_{n+1}}\right)\right\}=10\left(\frac{1}{a_1}-\frac{1}{a_{n+1}}\right)=10\left[10-\frac{1-\frac{1}{{10}^2}}{\frac{1}{10}\left\{1-\frac{1}{{10}^{2\left(n+1\right)}}\right\}}\right]=\frac{1-\frac{1}{{10}^{2n}}}{1-\frac{1}{{10}^{2n+2}}}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a4bd52877826782c69edb6098ac4819d_l3.png)
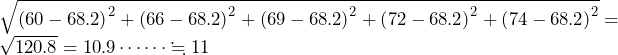 ……(答)
……(答)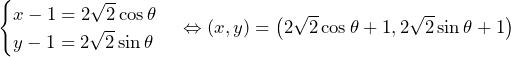 とおくことができる(
とおくことができる(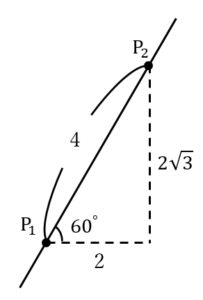
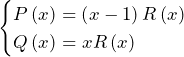 ……(*)
……(*)