大問2 (1) この問題のポイントは、「正角形はその外接円の中心を頂点として、個の合同な三角形に分割して考える」ことです。そのような三角形に分割して考える理由は、以下の2点です。 ・四角形、五角形、…よりも三角形のほうが簡単に扱える(計算できる)。 ・その三角形は明らかに二等辺三角形で、辺同士の関係
- …続きを読む
-
大問2
(1) この問題のポイントは、「正
 角形はその外接円の中心を頂点として、
角形はその外接円の中心を頂点として、 個の合同な三角形に分割して考える」ことです。そのような三角形に分割して考える理由は、以下の2点です。
個の合同な三角形に分割して考える」ことです。そのような三角形に分割して考える理由は、以下の2点です。・四角形、五角形、…よりも三角形のほうが簡単に扱える(計算できる)。
・その三角形は明らかに二等辺三角形で、辺同士の関係、面積が簡単に分かる。
私たちは、三角形や、綺麗な四角形(長方形など)の面積の公式を知っていても、一般の五角形や六角形の面積の公式を学習する機会はありません。では必要に迫られて五角形や六角形の面積、あるいは
 角形の図形の面積を導出しなければならないとき、どうすればよいでしょうか。いくつかの三角形に分割すれば、私たちが知っている三角形の面積の公式を使って求めることができます。このように、三角形は、他のどんな多角形よりも扱いやすいのです。よって1点目の考え方があります。
角形の図形の面積を導出しなければならないとき、どうすればよいでしょうか。いくつかの三角形に分割すれば、私たちが知っている三角形の面積の公式を使って求めることができます。このように、三角形は、他のどんな多角形よりも扱いやすいのです。よって1点目の考え方があります。また、2点目については、そのように分割することで頂角の大きさが
 の2等辺三角形が
の2等辺三角形が 個できることは明らかです。また、頂角の向かいの辺の長さは
個できることは明らかです。また、頂角の向かいの辺の長さは を使うと、
を使うと、 と表せます。また、余弦定理や三角比を使うことにより、残りの辺の長さを
と表せます。また、余弦定理や三角比を使うことにより、残りの辺の長さを とおけば、頂角の大きさと
とおけば、頂角の大きさと で
で を表せます。面積についても同様です。
を表せます。面積についても同様です。(2) 基本的な極限の計算です。(1)で2倍角/半角の公式を使うことにより、最終的な答えを簡単にしておいたほうが計算しやすいです。
(3)解答例では、
 を
を に置きかえることにより、
に置きかえることにより、 を
を の関数とみなして大小関係を比べました。この方法は、左辺から右辺(右辺から左辺)を引いて正か負か判別しにくいときに有効です。今回の場合、関数に置き換えることで、「微分」できるようになりました。微分することにより、考えている関数の変化の様子、特に増減の様子が分かるのでこの方針と問題の相性は抜群です。
の関数とみなして大小関係を比べました。この方法は、左辺から右辺(右辺から左辺)を引いて正か負か判別しにくいときに有効です。今回の場合、関数に置き換えることで、「微分」できるようになりました。微分することにより、考えている関数の変化の様子、特に増減の様子が分かるのでこの方針と問題の相性は抜群です。解答例

(1) 図のような、正
 角形の外接円の半径を
角形の外接円の半径を とし、
とし、隣り合う2つの頂点と外接円の中心を結んだ二等辺三角形を考える。その三角形の底辺の長さが
 、残りの2辺の長さが
、残りの2辺の長さが 、頂角の大きさが
、頂角の大きさが であることは明らかである。
であることは明らかである。そこで、頂角の2等分線を引くと、図のように互いに合同な直角三角形に分割できる。
その合同な三角形の辺の関係を考えれば、
 が成立する。
が成立する。また、その三角形の面積を考えることにより、
 が成立する。
が成立する。これを、
 を消去できるように変形すると、
を消去できるように変形すると、 により、
により、 である。
である。よって、

(2)
 であり、
であり、 、
、 より、
より、
 なので、
なので、
(3) 関数
 を考える。
を考える。
さらに、分子について、
 とおくと、
とおくと、 で、単調増加することがわかる。
で、単調増加することがわかる。 より、
より、 が正のとき、
が正のとき、
また、
 が正のとき、
が正のとき、 なので、
なので、 であることがわかる。
であることがわかる。 のとき、
のとき、 である。
である。 は
は が正のとき、単調増加するから、
が正のとき、単調増加するから、
すなわち、
 が従う。
が従う。解説
(1) 方針に従って計算しました。次の(2)が極限の問題なので、それを見据えて2倍角/半角の公式を使い、極限を求めやすい式にしています。
(2) 公式
 を、
を、 と置き換えて使いました。
と置き換えて使いました。(3) 方針に従って計算しました。
 をそのまま
をそのまま と置き換えても良いですが、
と置き換えても良いですが、 を
を と置き換えたほうが簡単に微分できます。
と置き換えたほうが簡単に微分できます。続きはこちらから

大問1
大問2
大問3
大問4
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。








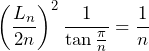 である。
である。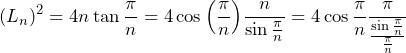 であり、
であり、