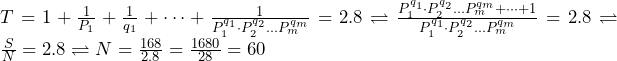方程式とはなにか? 方程式とは、値が分からない文字が入った等式のことです。 ”等式”というのは”等しい式”、つまり”=”で結ばれた式のことです。 この等式は文字にある値を代入したときに成り立ちます。 このように文字に代入して等式が成り立つ数のことを解といいます。 つまり、問題でよく見かける”方程式を
- …続きを読む
-
方程式とはなにか?
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]問題でよく”方程式を解け”って出てくるけど、そもそも方程式って何?[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]なんだろうね…。確かにあまり意識したことないや。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]とりあえず式の中の文字当てはまる数を求めてるけど…。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]その文字に当てはまる数を求めることを”方程式を解く”っていうんじゃない?”[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]じゃあ方程式ってそういう文字が入った式の事なのかな?[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]まあそんなもんじゃない?![/speech_bubble]方程式とは、値が分からない文字が入った等式のことです。
”等式”というのは”等しい式”、つまり”=”で結ばれた式のことです。
この等式は文字にある値を代入したときに成り立ちます。
このように文字に代入して等式が成り立つ数のことを解といいます。つまり、問題でよく見かける”方程式を解け”とは
’’この文字に代入してイコールが成り立つ値を求めて!”という意味なのです。
方程式の解き方
方程式と言っても様々な種類があります。
1次方程式、2次方程式、連立方程式、高次方程式、微分方程式などです。
1次方程式とは値が分からない数が一次の等式のことです。
ここでは最もシンプルな方程式である1次方程式についてだけ、説明します。”一次”というのはx, y, a, bなどなど、式の中の文字が、1乗までしかないってことです!
x², y³のように、に2乗3乗の文字はない、まあいたってシンプルな感じのやつですね。では解き方について簡単に説明です!
①カッコを展開したり移項をしたりして、xのついたやつを全部左側に持っていく。
②イコールの両辺に同じ数をかけたり割ったりして、
x=(ある数)
とする!これで求まります。
と日本語で言っても何言ってるのかわかりませんね。
数学は数字が言語ですから(嫌だとか言わないで(ToT))実際にやってみましょう。方程式の例題
問題:方程式 3(x+5)=12 の解をもとめよ。
答え:上のステップと照らし合わせてやってみます。
①カッコを展開する 3x+15=12
15を移項する 3x=12-15
3x=-3 ←左側がxだけの式になった!②両辺を3で割る x=-1
答えはx=-1です! もとの方程式に代入して確かめて見てください。確かに成り立ってますね。
ところで最初の段階で、「え、展開するの…?」と思った方、なかなか手慣れていますね。
実はこの問題の場合、最初に両辺を3で割ってしまうと大変簡単に求まってしまいます!
つまり、
3(x+5)=12
x+5=4
x=-1という具合です!こっちのほうが数字が小さくてなんだか気持ちが良いと思いませんか?
でもこうやって最初の式の段階で両辺を同じ数で割れることはそんなに多くありません。
割るときはほんとに割れるか確かめてからですよ!方程式を解く際のポイント
これは本当に本当に基本的な1次方程式の解き方です。
他に、分数や小数、ときにはルート(√2とかそういうやつ)が入ってくるものもあります。
ここではそんなに全パタ−ンを紹介することはとてもできないので、みなさんお手持ちの教科書や問題集などでの練習が不可欠です。しかしどんな問題でも、基本は
★カッコの展開、移項
★両辺を同じ数でかける、割る
の操作だけで完了できます!どの操作をしたら x= ◯ というゴールの形に近づけるか考えて、少しずつ計算に慣れていきましょう!
方程式は数学の基本ですが、方程式と同じくらい重要な概念に不等式もあります。不等式についてはこちらの記事をどうぞ!
[nlink url="https://hiroacademia.jpn.com/blog/5minutes/5minmt/hutoshiki/"]