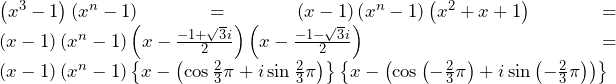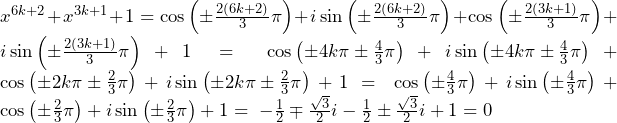慶應義塾大学過去問徹底研究 2018年 大問1 方針の立て方 (1) 頻出問題のため特筆事項なし.(を使うにはが必要だから,方程式全体をの何乗かで割るということに気付くこともできる.) (2) 与えられた条件式が対称式であるため,とで表せると考え,変形する.また,とに課せられた条件は,のみではなく「
- …続きを読む
-
慶應義塾大学過去問徹底研究 2018年 大問1
方針の立て方
(1)
頻出問題のため特筆事項なし.( を使うには
を使うには が必要だから,方程式全体を
が必要だから,方程式全体を の何乗かで割るということに気付くこともできる.)
の何乗かで割るということに気付くこともできる.)(2)
与えられた条件式が対称式であるため, と
と で表せると考え,変形する.また,
で表せると考え,変形する.また, と
と に課せられた条件は,
に課せられた条件は, のみではなく「実数である」ことにも注意.この問題も頻出問題である.
のみではなく「実数である」ことにも注意.この問題も頻出問題である.(3)
 も
も もまだ因数分解できるため,一先ず因数分解をし切って,共通因数を除外して考える.「割ること」を考えているため,和→積の変形である因数分解をなるべくしておくと良いことには気付きたい.そうすると,
もまだ因数分解できるため,一先ず因数分解をし切って,共通因数を除外して考える.「割ること」を考えているため,和→積の変形である因数分解をなるべくしておくと良いことには気付きたい.そうすると, と
と で割り切れることを示せれば十分と分かるため,因数定理に持ち込む方針が得られる.更に複素数の
で割り切れることを示せれば十分と分かるため,因数定理に持ち込む方針が得られる.更に複素数の 乗の計算を求められるため,ド・モアブルの定理を使うことも見抜きたい.
乗の計算を求められるため,ド・モアブルの定理を使うことも見抜きたい.解答例
(1)
ア:
イ:
(2)
ウ:
エ:
(3)

 と書ける.
と書ける.


より, のとき,
のとき, となれば,因数定理より
となれば,因数定理より は
は と
と の両方を因数に持つことになり,
の両方を因数に持つことになり, で割り切れることが示せる.
で割り切れることが示せる.

であり, を代入すると,ド・モアブルの定理より,
を代入すると,ド・モアブルの定理より,

となり,題意が示せた. 証明終了.解説
(1)
〇 の満たす2次方程式(アについて)
の満たす2次方程式(アについて)
 は解とならない.よって,方程式の両辺を
は解とならない.よって,方程式の両辺を で割ることができ,
で割ることができ,

よって,求める2次方程式は,
 ……(答)
……(答)
〇方程式の解(イについて)
 を解くと
を解くと .
.


これを解くと,
 ……(答)
……(答)(2)
〇 の式(ウについて)
の式(ウについて)


ここで, は上式を満たさないため,
は上式を満たさないため, .この下で上式を
.この下で上式を について解くと,
について解くと,
 ……(答)
……(答)
〇 のとりうる値の範囲(エについて)
のとりうる値の範囲(エについて)
 より,
より, は次の
は次の についての2次方程式の2解である.
についての2次方程式の2解である.

 が実数であるには,この2次方程式の判別式が0以上であれば必要十分である.
が実数であるには,この2次方程式の判別式が0以上であれば必要十分である.

 より,
より,

 より,求める条件は,
より,求める条件は,
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。