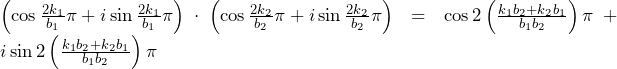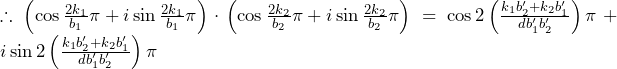早稲田大学理工過去問徹底研究 2017年 大問4 方針の立て方 (1) まずはの表式を求めることを考える.はとの二文字の式であるが,与えられた関係式(漸化式)がを固定してを動かしていることから,はについての数列と見て考えるのがよさそうだと気付く.この漸化式は普通に解けるタイプのものではないから,試し
- …続きを読む
-
早稲田大学理工過去問徹底研究 2017年 大問4
方針の立て方
(1)
まずは の表式を求めることを考える.
の表式を求めることを考える. は
は と
と の二文字の式であるが,与えられた関係式(漸化式)が
の二文字の式であるが,与えられた関係式(漸化式)が を固定して
を固定して を動かしていることから,
を動かしていることから, は
は についての数列と見て考えるのがよさそうだと気付く.この漸化式は普通に解けるタイプのものではないから,試しに
についての数列と見て考えるのがよさそうだと気付く.この漸化式は普通に解けるタイプのものではないから,試しに や
や ,
, 等を求めると,解法を得られる.数列の問題は代入して解法を得られることが多いため,困ったら代入して計算してみよう.
等を求めると,解法を得られる.数列の問題は代入して解法を得られることが多いため,困ったら代入して計算してみよう.
また,シグマ内のコンビネーションは二項定理で変形することも重要な解法であるためおさえておくこと.(2)
「 が確率である」という情報を使っていないことに気付ければ解法が得られる.確率の総和は1であるから,前問の解答と=にすればよい.
が確率である」という情報を使っていないことに気付ければ解法が得られる.確率の総和は1であるから,前問の解答と=にすればよい.
(3)
今度は を固定して
を固定して を動かす.要は,
を動かす.要は, は
は の一変数関数であるから,微分をして求めればよい.
の一変数関数であるから,微分をして求めればよい.(4)
代入して計算する.やはりシグマ内のコンビネーションが出てくるため,これを二項定理で変形する.解答例
(1)
まず, であることを
であることを についての数学的帰納法で示す.
についての数学的帰納法で示す.
 のとき,(右辺)
のとき,(右辺) .よって,成立.
.よって,成立.
 (
( は
は を満たす自然数)のときの成立を仮定.つまり,
を満たす自然数)のときの成立を仮定.つまり, を仮定する.
を仮定する.
すると,
 (
( 漸化式)
漸化式) (
( 帰納法の仮定)
帰納法の仮定)
となり,これは での成立を意味する.
での成立を意味する.
以上,数学的帰納法により であることが示せた. 証明終了.
であることが示せた. 証明終了.
さて,途中で二項定理を用いれば,
 ……(答)
……(答)(2)
 より,
より, は全事象の確率の和である.
は全事象の確率の和である.


 より,
より,
 ……(答)
……(答)(3)

 のとき,
のとき,

よって,
増減表を描くと,













最大 

 のとき,
のとき, より,
より,
 のとき,
のとき, より,
より,
よって,全ての に対して,
に対して,
 ……(答)
……(答)(4)
 (二項定理)
(二項定理)
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。








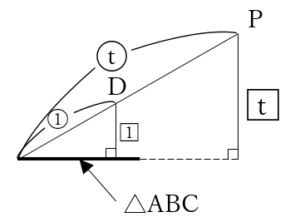
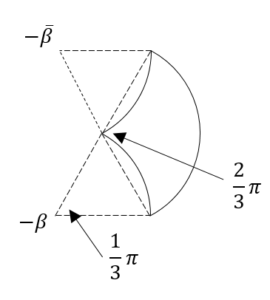
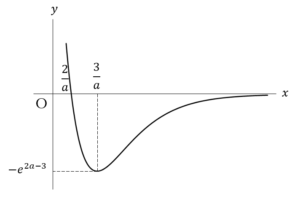 (上図が答え)
(上図が答え)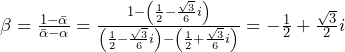 ……(答)
……(答)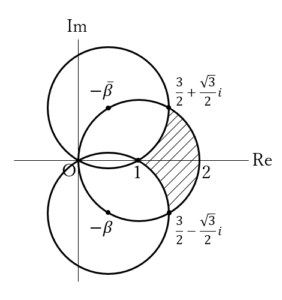
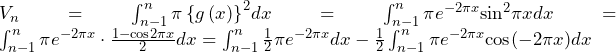
![Rendered by QuickLaTeX.com \int_{n-1}^{n}{\pi e^{-2\pi x}\cos{\left(-2\pi x\right)}}dx=-\frac{1}{2}\int_{-2\left(n-1\right)\pi}^{-2n\pi}{e^y\cos{y}}dy\bigm=-\frac{1}{2}\left[\frac{1}{2}e^y\left(\cos{y}+\sin{y}\right)\right]_{-2\left(n-1\right)\pi}^{-2n\pi}\bigm=-\frac{1}{4}\left(e^{-2n\pi}-e^{-2\left(n-1\right)\pi}\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-df13329429bcde4e2ecc7f39a38e588b_l3.png)
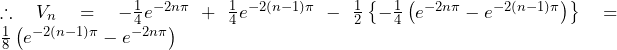 ……(答)
……(答)
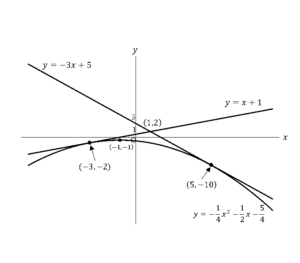
![Rendered by QuickLaTeX.com \int_{-3}^{1}\left\{\left(x+1\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx+\int_{1}^{5}\left\{\left(-3x+5\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx\bigm=\left[\frac{1}{12}x^3+\frac{3}{4}x^2+\frac{9}{4}x\right]_{-3}^1+\left[\frac{1}{12}x^3-\frac{5}{4}x^2+\frac{25}{4}x\right]_1^5=\frac{32}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-bbec6b7afbfd51917ee8a7761b2bc8b3_l3.png) ……(答)
……(答)



 (
(