方針の立て方 (1) およびで割り切れるということはで割り切れるということである.これに気付けなくとも,と表せることから,はを因数に持ち,はを因数に持つということが分かれば,結局同じ議論ができる.後は,本解答のようにを導入し解析していく.の導入は「がで割り切れる」という情報と「がで割り切れる」という
- …続きを読む
-
方針の立て方
(1)
 および
および で割り切れるということは
で割り切れるということは で割り切れるということである.これに気付けなくとも,
で割り切れるということである.これに気付けなくとも, と表せることから,
と表せることから, は
は を因数に持ち,
を因数に持ち, は
は を因数に持つということが分かれば,結局同じ議論ができる.後は,本解答のように
を因数に持つということが分かれば,結局同じ議論ができる.後は,本解答のように を導入し解析していく.
を導入し解析していく. の導入は「
の導入は「 が
が で割り切れる」という情報と「
で割り切れる」という情報と「 が
が で割り切れる」という情報の両方ともを加味しているため,
で割り切れる」という情報の両方ともを加味しているため, と
と で考えるよりも都合が良い.
で考えるよりも都合が良い.
求めるのは最小の次数のものであるため, を0次,1次,2次,……と考えていけば良い.
を0次,1次,2次,……と考えていけば良い.(2)(3)は,(1)で
 が特定できてしまえば,典型問題の三次関数の接線の問題となる.特に捻りもなく,典型的な解法を取れば良い.
が特定できてしまえば,典型問題の三次関数の接線の問題となる.特に捻りもなく,典型的な解法を取れば良い.解答例
 と表せる.
と表せる.
(1)
 で割り切ることができる.その商を
で割り切ることができる.その商を とおく.
とおく.
すると,

と表せる.
これより,
 ……(*)
……(*)
となる.
 より,(*)の上式に
より,(*)の上式に を代入すると,
を代入すると,

 より,(*)の下式に
より,(*)の下式に を代入すると,
を代入すると,

よって,

これを満たす で次数が最小のものは,
で次数が最小のものは, である.
である.
 ……(答)
……(答)(2)
 であるから,
であるから, である.
である.
よって,点 における接線は,
における接線は,

よって,求める傾きは ,
, 切片は
切片は ……(答)
……(答)(3)
接線 が点
が点 を通るので,
を通るので,
 ……(※)
……(※)
が成り立つ.
 は三次関数であり,複接線は引けないから,接線の本数と接点の個数は等しくなる.よって,(※)を
は三次関数であり,複接線は引けないから,接線の本数と接点の個数は等しくなる.よって,(※)を の三次方程式
の三次方程式

の解がちょうど2個存在すれば必要十分である.

とおくと,

である.
(ⅰ) のとき
のとき
 となり,
となり, (等号成立は
(等号成立は のときのみ)であるから
のときのみ)であるから は単調増加となる.このとき,
は単調増加となる.このとき, となる
となる はただ1つしか存在しないため不適.
はただ1つしか存在しないため不適.
(ⅱ) のとき
のとき
 となる
となる は2つ(
は2つ( )あり,かつ
)あり,かつ それぞれの前後で
それぞれの前後で の符号が変化するから,
の符号が変化するから, は極大値を極小値を1つずつ持つ(
は極大値を極小値を1つずつ持つ( のどちらが極大値,極小値になるかは
のどちらが極大値,極小値になるかは と1の大小関係に依存する).この極大値もしくは極小値が0となるとき,
と1の大小関係に依存する).この極大値もしくは極小値が0となるとき, となる解はちょうど2つ存在し,題意を満たす.
となる解はちょうど2つ存在し,題意を満たす.


より,極大値もしくは極小値が0となるのは,
 または,
または,
のとき.
以上,(ⅰ)と(ⅱ)より,求める条件は,
 または,
または, (ただし,
(ただし, )……(答)
)……(答)







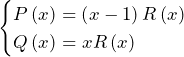 ……(*)
……(*)

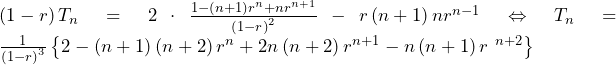 ……(答)
……(答)![Rendered by QuickLaTeX.com \int_{0}^{2}\left(-6x+15\right)dx=\left[-3x^2+15x\right]_0^2=18,\int_{0}^{2}\left(-3x^2+12\right)dx=\left[-x^3+12x\right]_0^2=16](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c3bfa33edb30774157f6fafbfffed269_l3.png)
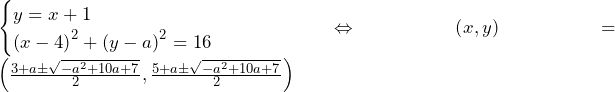 (複号同順)
(複号同順)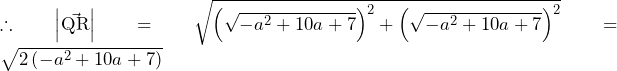
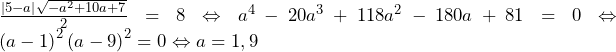 ……(答)
……(答)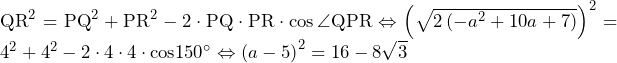 ……(答)
……(答)