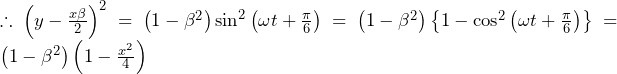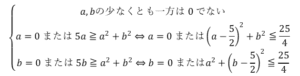早稲田大学理工過去問徹底研究 2018年 大問2 方針の立て方 (1) 領域の図示も求積も頻出問題のため特筆事項なし.図示する場合には共有点はきちんと出しておくようにしよう. (2) 領域はの範囲に限られるため,は高々9通りを考えれば良い.そのためトリッキーな解法を考えるよりも,虱潰しに数え上げた方
- …続きを読む
-
早稲田大学理工過去問徹底研究 2018年 大問2
方針の立て方
(1)
領域の図示も求積も頻出問題のため特筆事項なし.図示する場合には共有点はきちんと出しておくようにしよう.(2)
領域は の範囲に限られるため,
の範囲に限られるため, は高々9通りを考えれば良い.そのためトリッキーな解法を考えるよりも,虱潰しに数え上げた方が速いと判断し,地道に数え上げる.
は高々9通りを考えれば良い.そのためトリッキーな解法を考えるよりも,虱潰しに数え上げた方が速いと判断し,地道に数え上げる.解答例
(1)

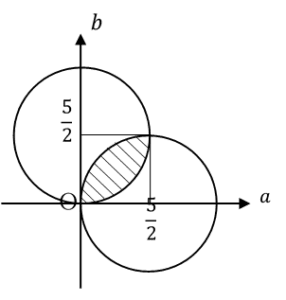
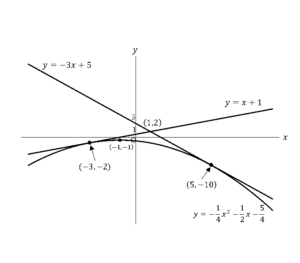
これを図示すると,

(なお, と
と で,放物線は直線と接する.)
で,放物線は直線と接する.)
よって,求める面積は,
![Rendered by QuickLaTeX.com \int_{-3}^{1}\left\{\left(x+1\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx+\int_{1}^{5}\left\{\left(-3x+5\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx\bigm=\left[\frac{1}{12}x^3+\frac{3}{4}x^2+\frac{9}{4}x\right]_{-3}^1+\left[\frac{1}{12}x^3-\frac{5}{4}x^2+\frac{25}{4}x\right]_1^5=\frac{32}{3}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAogAAAA4AQAAAABWZzRLAAAAAnRSTlMAAHaTzTgAAAAbSURBVFjD7cEBDQAAAMKg909tDwcUAAAAAE8GEfAAAdb+/VcAAAAASUVORK5CYII=) ……(答)
……(答)(2)
 から
から まで,
まで, を一つずつ動かしながら考える.
を一つずつ動かしながら考える.
 ……0個
……0個
 ……0個
……0個
 ……0個
……0個
 ……2個
……2個
 ……3個
……3個
 ……2個
……2個
 ……0個
……0個
 ……0個
……0個
 ……0個
……0個
よって,求める個数は 個……(答)
個……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







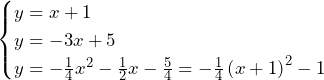
![Rendered by QuickLaTeX.com \int_{-3}^{1}\left\{\left(x+1\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx+\int_{1}^{5}\left\{\left(-3x+5\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx\bigm=\left[\frac{1}{12}x^3+\frac{3}{4}x^2+\frac{9}{4}x\right]_{-3}^1+\left[\frac{1}{12}x^3-\frac{5}{4}x^2+\frac{25}{4}x\right]_1^5=\frac{32}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-bbec6b7afbfd51917ee8a7761b2bc8b3_l3.png) ……(答)
……(答)

 (
(
![Rendered by QuickLaTeX.com \therefore\left\{\min_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx\leqq a_k\leqq\left\{\max_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f36be33140d882a415e9c83b4517d00d_l3.png)
![Rendered by QuickLaTeX.com \int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx=\left[-\frac{1}{\left(2n+1\right)\pi}\cos{\left(\left(2n+1\right)\pi x\right)}\right]_{x_k}^{x_{k+1}}\bigm=\frac{\left(-1\right)^k-\left(-1\right)^{k+1}}{\left(2n+1\right)\pi}\bigm=\frac{2}{\left(2n+1\right)\pi}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c2feed9a41ae6737010103dd006acf33_l3.png) (∵
(∵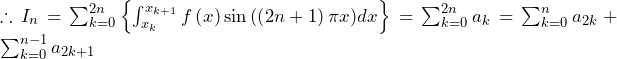
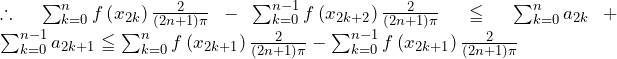
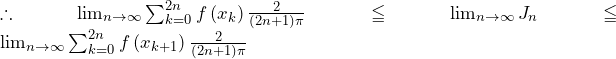
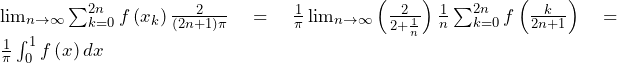
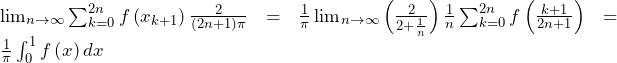
 ……(答)
……(答)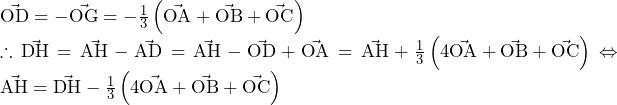
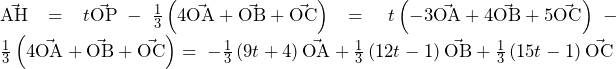 ……(答)
……(答)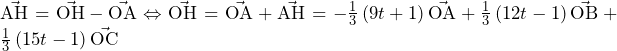
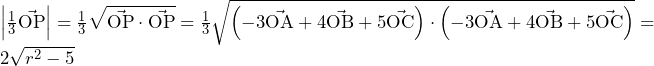
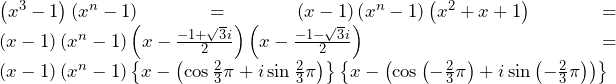
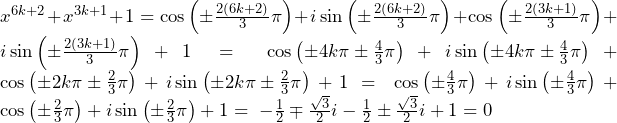
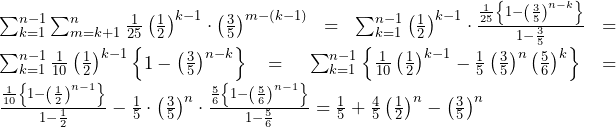 ……(答)
……(答)