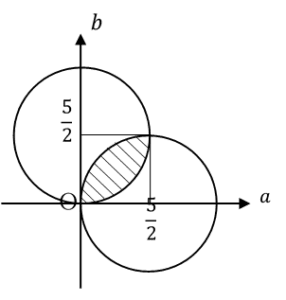
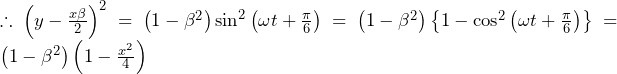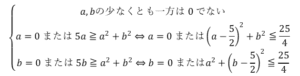2017年慶應大学理工|過去問徹底研究 大問5 方針の立て方 (1) (フ)については,「方程式の解」⇔「関数と軸との交点(の座標)」の同値変形を利用する.典型的な解法であるため,これ以上の特筆事項なし. (ヘ)については,増減表が描けていれば素直に計算するのみ. (2) (ホ)も問題文に素直に従い
- …続きを読む
-
2017年慶應大学理工|過去問徹底研究 大問5
方針の立て方
(1)
(フ)については,「方程式 の解」⇔「関数
の解」⇔「関数 と
と 軸との交点(の
軸との交点(の 座標)」の同値変形を利用する.典型的な解法であるため,これ以上の特筆事項なし.
座標)」の同値変形を利用する.典型的な解法であるため,これ以上の特筆事項なし.
(ヘ)については,増減表が描けていれば素直に計算するのみ.(2)
(ホ)も問題文に素直に従い,法線を出し,それと との交点を計算すれば求まる.
との交点を計算すれば求まる.
(マ)については,最小値問題で最初に疑う相加・相乗平均の関係式で解ける問題であり,特筆事項なし.(ミ)について.「接線」が「法線」となっただけで,三次関数の接線の本数問題と同様の解き方をすればよいと考える.(1)の問題の結果を利用していないことを気に留めておくと途中の計算を殆どせずに答えにたどり着く.
解答例
(1)
フ:
ヘ:
(2)
ホ:
マ:
ミ:
解説
(1)
〇 の条件(フについて)
の条件(フについて)
 とおくと,
とおくと,


増減表をかくと,x 






0 
0 






よって,3次方程式
 が,ただ1つの実数解を持つ条件は,
が,ただ1つの実数解を持つ条件は,

この内, ,
, より,常に成立しない.
より,常に成立しない.
 ……(答)
……(答)
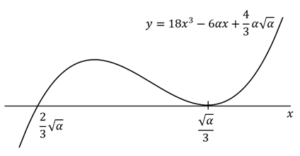
〇面積(ヘについて)
 のとき,
のとき,

よって,グラフの概形は下図の通り.

求める面積は,
![Rendered by QuickLaTeX.com \int_{-\frac{2}{3}\sqrt\alpha}^{\frac{\sqrt\alpha}{3}}\left(18x^3-6\alpha x+\frac{4}{3}\alpha\sqrt\alpha\right)dx=\left[\frac{9}{2}x^4-3\alpha x^2+\frac{4}{3}\alpha\sqrt\alpha x\right]_{-\frac{2}{3}\sqrt\alpha}^{\frac{\sqrt\alpha}{3}}\bigm=\frac{3}{2}\alpha^2](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAksAAAApAQAAAAANZVDXAAAAAnRSTlMAAHaTzTgAAAAZSURBVEjH7cEBAQAAAIIg/69uSEABAABHBgwDAAG/MuAeAAAAAElFTkSuQmCC) ……(答)
……(答)(2)
〇 (ホについて)
(ホについて)

これより,点Pでの接線の傾きは であり,法線の傾きは,
であり,法線の傾きは, と分かる.よって,点Pでの法線の方程式は,
と分かる.よって,点Pでの法線の方程式は,

これと, の交点の
の交点の 座標は,
座標は,

 より,
より,
 ……(答)
……(答)
〇 の最小値(マについて)
の最小値(マについて)

 かつ
かつ より,相加・相乗平均の関係式が使えて,
より,相加・相乗平均の関係式が使えて,

等号成立は, に注意すれば,
に注意すれば,

で成立する.
よって,求める最小値は ……(答)
……(答)
〇 (ミについて)
(ミについて)
前問の議論より,点Pでの法線の方程式は,

であった.
よって, についての以下の方程式
についての以下の方程式
 が,ただ1つの実数解をもつ条件を考えれば必要十分.
が,ただ1つの実数解をもつ条件を考えれば必要十分.
① のとき
のとき
 ,
, とすることで,(1)の議論に帰着でき,考えるべき条件は,
とすることで,(1)の議論に帰着でき,考えるべき条件は,

と分かる.
② のとき
のとき
 ,
, とすることで,(1)の議論を考え直すと,
とすることで,(1)の議論を考え直すと,

となり,任意の に対してただ1つの実数解をもつ.
に対してただ1つの実数解をもつ.
よって,求める必要十分条件は,

である.
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。








![Rendered by QuickLaTeX.com \therefore\left\{\min_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx\leqq a_k\leqq\left\{\max_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f36be33140d882a415e9c83b4517d00d_l3.png)
![Rendered by QuickLaTeX.com \int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx=\left[-\frac{1}{\left(2n+1\right)\pi}\cos{\left(\left(2n+1\right)\pi x\right)}\right]_{x_k}^{x_{k+1}}\bigm=\frac{\left(-1\right)^k-\left(-1\right)^{k+1}}{\left(2n+1\right)\pi}\bigm=\frac{2}{\left(2n+1\right)\pi}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c2feed9a41ae6737010103dd006acf33_l3.png) (∵
(∵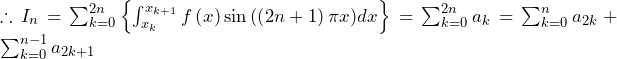
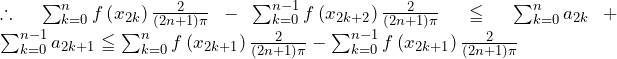
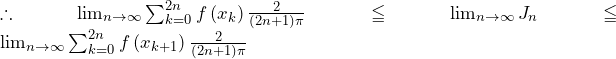
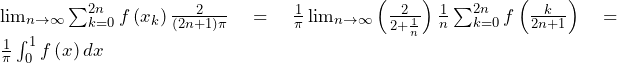
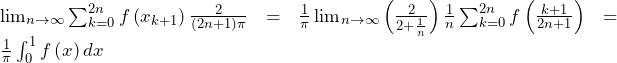
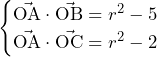
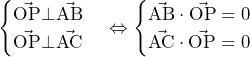
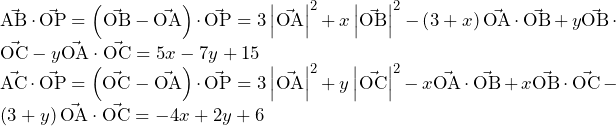
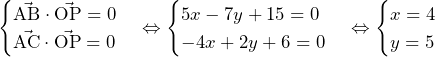 ……(答)
……(答)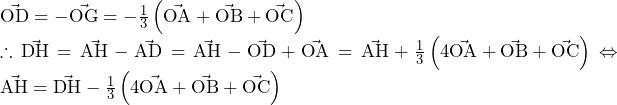
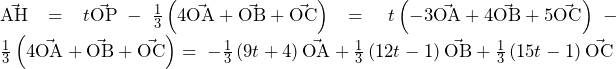 ……(答)
……(答)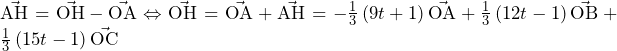
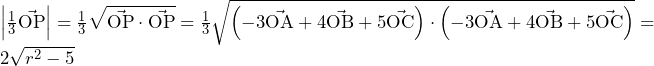
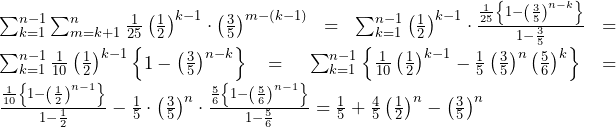 ……(答)
……(答)