このブログでは、慶應大学理工学部の数学に関する入試対策(出題傾向と勉強法、参考書)をご紹介していきます。
基礎知識0の状態から合格するためには何をどのようにしたら良いのかを参考書の使い方まで徹底解説!
ページ目次
慶應理工の数学の全体概観
理工学部の数学は基本事項の使い方が大切になってきます。
教科書に載っている基本事項を十分に活用できるようになる必要があります。
それに合わせて、いろいろな問題演習を通じて、
柔軟な思考力を養う必要もあります。
出題される大問は5題です。大部分はマークシートで、一部記述式です。
記述式の設問では、証明問題が毎年出題されます。
全て解き切るのは時間的に厳しいので、
問題を解くのに必要な処理量や計算力、難易度を見極める力も重要です。
難しい問題も多いですが、7割程度は取れる学力が必要です。


- 【何からはじめたらいい?という人向け】
【まず始めることをお伝えします】 - 早慶に合格するための戦略とは?
1,2年生から合格するための戦略を立てるには? - 【高1】早慶現役合格の勉強法を徹底解説
志望校に合格するためにやるべきこと紹介 - 【高2】現役で早慶GMARCHに合格
必要な勉強法(勉強時間、参考書)を紹介 - 【高2】早慶絶対合格!!のためにすること
勉強時間、スケジュール、参考書、勉強法の紹介
慶應理工の数学の出題範囲・頻出分野
理工学部の数学は、数学Ⅰ・数学Ⅱ・数学Ⅲ・数学A・数学B・数学Cからの出題で、
数学Aからは「場合の数と確率」・「整数の性質」・「図形の性質」、
数学Bからは「数列」
数学Cからは「ベクトル」「平面上の曲線と複素数平面」が出題範囲となっています。
頻出分野は当然ですが、、微積分です。
例年2題以上出題されており、計算量が多いのが特徴です。
また、微積分以外では、数列・確率・ベクトル・三角関数など
数Ⅰ・数A・数Bなどからもまんべんなく出題され、
いくつかの単元にわたる融合問題の出題も見られます。
全体的に数学Ⅲの分野が頻出であり、
また空間図形・確率漸化式など試験範囲が出せれているので、
全分野の学習について念入りな学習が必要です。
慶應理工の数学の頻出分野の対策方法

微積
微積は占める比重も大きいので、真っ先に固めたい分野です。
小問集合ないでも大問でも出題され、難易度はバラバラですが、
手がつけられないような難問は出題されないので確実に解きたい分野です。
最初の敷居は高いですが、
パターンが決まっているので一度得意にしてしまえば得点源にしやすいです。
また2014年度の大問5のように知っていれば、すぐに解くことができる問題も出題されます。
「x軸、y軸で切り取られる線分の長さが常に1」といわれたら…「アステロイドじゃないか?!」とひらめけるようになれるとよいでしょう。
このように微積には色々と背景があったり、有名な問題が多いので一通り当たって知識を蓄えておくと有利に働くことが多いです。
普段問題を解きっぱなしにするのではなく、
深く考察したり、
背景を調べてみたりすると数学の勉強が楽しくなると思います。
場合の数・確率
慶應では理工、薬、医において、場合の数・確率の出題が盛んです。
特にn絡み、漸化式の出題が毎年のようになされています。
高校ではしっかりと扱わないからか苦手意識を持っている人も多いのですが、
一度コツを掴んでしまえばスラスラできるようになります。
具体的にどう考えればいいのかはここでは扱いませんが、
理工の場合は医の問題の難易度に慣れておくと本番完答できるでしょう。
また東大の過去問を解くのもおすすめです。
空間
2014〜2017と4年連続で空間、立体の問題が大問で出ています。
ほとんどが四面体絡みで難易度はそこまで高くないものの
計算が大変な年もあり、試験場で思ったとおり進まない人も少なくありません。
立体は「適切な断面で切って、平面で考える」というのが定石なのですが、
本学は誘導が丁寧に与えられているため、そこの思考過程は問題ではありません。
なので基本的に誘導に乗るだけですが、
ベクトルと空間座標の基礎は理解しておく必要があります。
そして計算が大変でも焦らず、
地道に計算するクセを普段からつけておくと本番自身を持って解けます。
本学のレベルなら落とせないので、まずは図を書き、丁寧に考えてみましょう。

慶應理工の数学を攻略するための日頃の勉強法

- 早慶は浪人しても難しい!?
根本的に変えていく必要性とその方法を伝授 - 【早慶浪人】伸びないのはなぜ?
伸ばし方を説明 - ヒロアカの浪人生必勝必勝コース
基礎から合格するための勉強法 - 【早慶浪人】年間スケジュール
浪人生が早慶に合格するための計画の立て方とは - 【早慶】女子浪人が絶対に合格には
志望校に合格するためにやるべきこと紹介 - 【早慶】3月にやっておくこと
早慶を目指す浪人生が絶対に3月にやっておくことを紹介

慶應の理工学部に圧勝で合格するためにどのように日頃勉強をしていったら良いのかを勉強をする際のポイントを記載していきます。
基礎学力の徹底的な強化
数学力を身につけることが大事となりますが、そのためには基本的な問題が解けるようになることが重要です。
1つ1つの分野、特に頻出範囲である微分・積分は重点的に学習しましょう。
また、理工学部の数学の問題は計算量が多く、早く正確に解くことが求められます。
マークシート方式では考え方が正しくても、計算ミスなどで正しい結果が出ない場合は得点ができないので、要領よくミスがないように正解を出せるように日ごろから計算するときも意識する必要があります。
自身の計算ミスの癖を理解する
慶應義塾大学理工学部の数学は、
計算量が多いため、計算ミスをする可能性があります。
上記したとおり、日頃から計算ミスをしない工夫をすることは当然ですが、
自身がどういう部分で計算ミスが起こるのかを
確認しておく必要があるでしょう。

実際の問題に慣れる
問題演習に慣れてきたら、実際に過去問に取り組みましょう。
この際、本番通りの時間で解くことが大切です。
数学ではどの分野が何問目に出るかが分からないので、
時間を測って問題演習をし、
自分が解きやすいと思った問題から解き始めることが重要です。
大問前半の比較的易しい問題を確実に解答することで、得点を伸ばしていきましょう。
ただし、時間内に解けなかった問題もその後に問題演習として解くことも大事です。
時間内に解けなかった問題は必然的に苦手な問題であるため、
苦手をつぶす意味でも解けなかった問題の復習をしましょう。
また理工学部の問題は空所補充の問題が多いので
過去問や模擬試験を通じて形式になれることも大切です。

慶應理工で合格するためのおすすめ参考書
ある程度の基礎学力はついた前提(偏差値55~60程度)で、
そこから成績を上げるための教材をお伝えしていきます。
入試演習段階でおすすめの参考書は?
理系数学マスト160題か 1対1対応の数学がおすすめです。
どちらを使うかは状況によりますが、
1対1対応は、数学が得意でないなら独学では使いづらいです。
また冊数も多くなってしまうので大変です。
そのような場合は、理系数学マスト160題がわかりやすくて良いです。
数学が苦手でも理解しやすい解説となっています。
苦手な問題傾向がわかってきたら、
上記問題集以外でもチャートを使って苦手分野を無くすようにしてください。
Z会の理系数学入試の核心 標準編も復習がしやすいのでおすすめです。
森本先生の教材とみてみてどちらか自分が使いやすい方をやってみると良いでしょう。
さらにやり込みたい!という人の参考書は・・
やさしい理系数学や毎年出る! センバツ40題 理系数学上位レベル[数学I・A・II・B・III] をやってみると良いでしょう。
両者とも慶應理工数学を考えるとやややり込みすぎですが、
数学を得意科目にしたい!という人はやってみた方が良いでしょう。
ただし、他の科目との兼ね合いを考えるのが重要です。
特に逆転合格を考えている人は難しい参考書をやるよりも
これまでの教材の復習を何度も何度もやりこむ方が効果は高いので
注意してください。
慶應理工学部の数学で圧勝する人はこう考える!

実際に問題を見て、問題を解くことができる人はどのように考えているのかを確認してください。できない人は上記の法則を利用することができていません。
実際に過去問を用意して考えてみましょう。
まず、初級編の2014年度の大問4に取り掛かってみましょう。

空間で大事な知識をまずチェックして起きましょう!
■直線のパラメーター(媒介変数)表示
![]() ,
,![]() は一次独立のベクトルとする。
は一次独立のベクトルとする。
※一次独立:簡単に言うと![]() ,
,![]() が全く違う方向に向いているということです。
が全く違う方向に向いているということです。
平面上の点(x)は任意の実数s,tを持ってくると
![]() ・・・(*)
・・・(*)
と表せます。
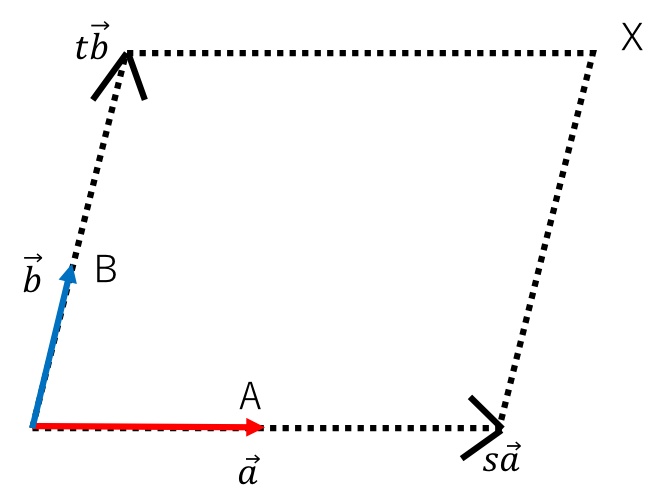
図1
(*)をs=1としたときにXは
![]()
![]() ・・・(☆)
・・・(☆)
でこれは図2のようにAを通りベクトル![]() に平行な直線となります。
に平行な直線となります。
 図2
図2
逆にtがすべての実数を取るときに![]() の集合は直線
の集合は直線![]() 全体になります。
全体になります。
(☆)には図2のAを原点として、OBの長さ(![]() )を1とする数直線を設定したときの目盛りを表すというイメージがわきます。
)を1とする数直線を設定したときの目盛りを表すというイメージがわきます。
さて、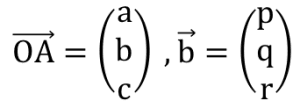
としても当てはまりますから(☆)を空間に拡張すると


図3
と表せます。(図3)すごく当たり前なのですが、
(a,b,c),(p,q,r)が分かっていてどれかの座標成分に決定的な情報があればtを求めることで、直線上の点が分かります。
平面から空間へ次元が上がると難しく思うかもしれませんが、おこなうことはほとんど変わりません。
本問はこれさえしっかりおさえておけば解けます。

解答編になります!
◯0 < t ≦ 1のとき
 なので、線分OA上にz=tを満たす点A’が存在する。
なので、線分OA上にz=tを満たす点A’が存在する。![]() 上の点Xは実数pを用いて
上の点Xは実数pを用いて![]() でz=3p=tより、
でz=3p=tより、![]() 上でz座標がtの点B’は
上でz座標がtの点B’は と表せる。
と表せる。
以上を踏まえると、f(t)は図5のようにかけるので、![]() ・・・(ソ)
・・・(ソ)
 図4
図4

図5
◯1<t<3のとき
 で線分OA上にz=tを満たす点が存在しなく、線分AB、AC、OCを共通にもつ。
で線分OA上にz=tを満たす点が存在しなく、線分AB、AC、OCを共通にもつ。
直線AB、AC上に点Y、Zは実数q,rを用いて
 ・・・(タ)
・・・(タ)
1+2q=t、1+2r=tを満たすとき![]() なのでこれを代入して
なのでこれを代入して

①、②を踏まえるとf(t)は図3のようにかけるので
![]() ・・・(チ)
・・・(チ)
 図6
図6
以上から
![]() ・・・③
・・・③
■ここで各々積分を実行したくなりますが、それは得策ではありません。
問題は、あとはg’(x)についてしかきいてませんから、③をそのまま微分すればよいです。
![]() ・・・③
・・・③
![]()
![]() ・・・(ツ)
・・・(ツ)
![]()
なのでg(t)は![]() で最大値をとります。(図7)
で最大値をとります。(図7)
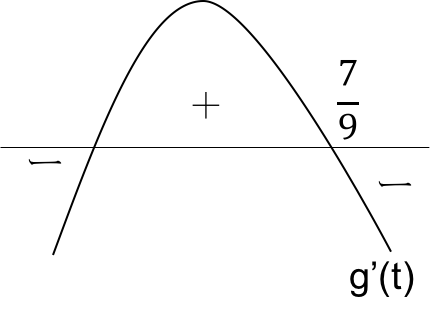 図7
図7

LINEでも、慶應理工に合格するためのおすすめの勉強の仕方をお伝えしているのでぜひ登録してくださいね。こちらから登録できます。

【応用編】2015年の大問4

20分を目安に取り組んでみてください。
(解)
(i)六面体OP1P2P3-P4P5P6P7は立方体(図8)
(ii)Pkのz座標が正
(iii)
(iv)P3がzx平面にある(⇆P3のy座標は0)
(iv)より とおける。(i)より
とおける。(i)より![]() かつ
かつ![]()
⇆![]() かつ2a+4b=0・・・①
かつ2a+4b=0・・・①
でaを消去するとb2=9で(ii)よりb=3
①に代入してaを求めると ・・・(ソ)
・・・(ソ)

図8
◯P4について
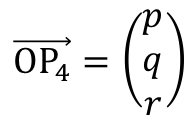 とおくと、
とおくと、
![]() かつ
かつ![]() かつ
かつ![]()
⇔2p + 5q + 4r = 0かつ-6p + 3r = 0かつp2 + q2 + r2 = 45
⇔q = -2pかつr = 2pかつp2 + q2 + r2 = 45
q,rを消去してpについて解くと![]() だが
だが![]() なので
なので![]()
である。よって
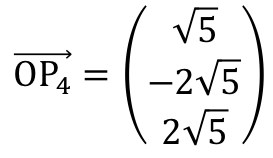 ・・・(タ)
・・・(タ)
◯P6について
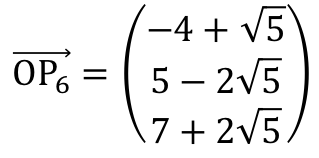 ・・・(チ)
・・・(チ)
◯四角形OQ1Q2Q3と六角形Q1Q2Q3Q7Q4Q5について図示すると図9のようになります。
(正方形をある面に投射すると平行四辺形になる。正方形は平行四辺形の中の1つ)
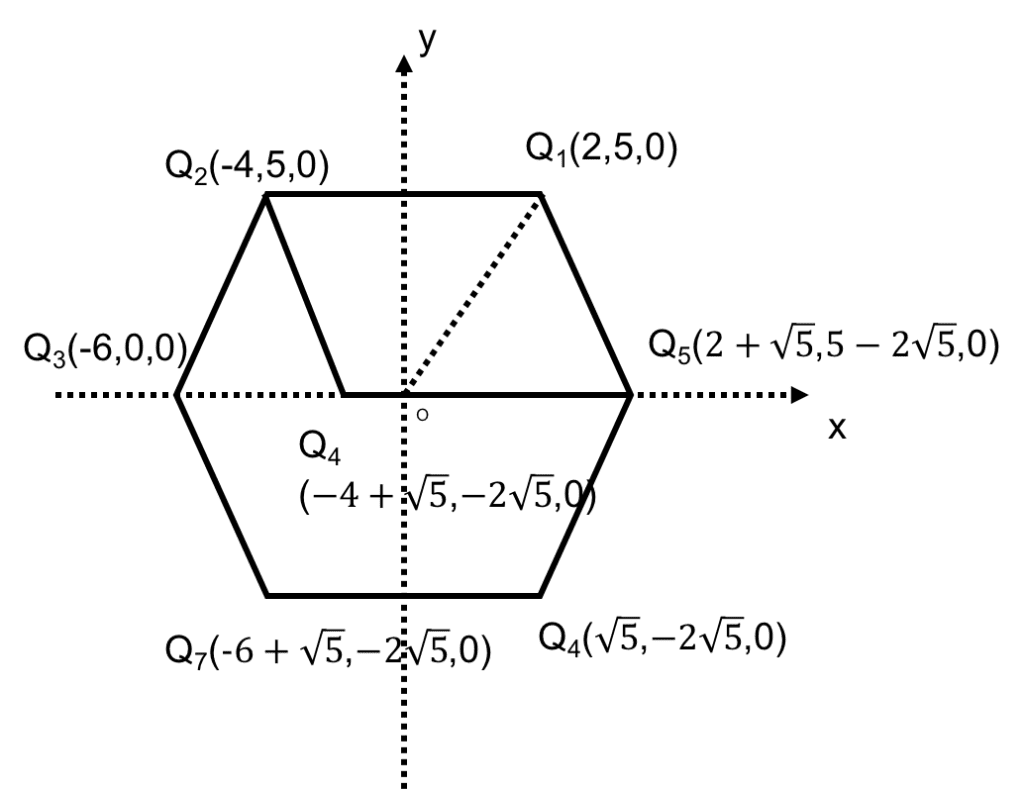
図9
平行四辺形OQ1Q2Q3=5・6=30・・・(ツ)
平行四辺形OQ3Q7Q4=![]()
平行四辺形OQ1Q5Q4=![]() より
より
六角形Q1Q2Q3Q7Q4Q5=![]() ・・・(テ)
・・・(テ)
◯立方体とz軸の交わりの線分の長さについて
いまz軸は原点を通るxy平面に垂直な直線であり図9から平行四辺形Q6Q5Q4Q7が原点Oを含むから平面P4P5P6P7がz軸と交点を持つ。
平面P4P5P6P7上の点Xは
![]() (t,sは任意の実数)
(t,sは任意の実数)
![]()
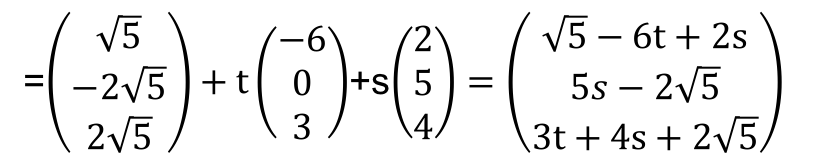
z軸はx=0,y=0なので![]() で交点の座標はで線分の長さは
で交点の座標はで線分の長さは![]() ・・・(ト)
・・・(ト)

慶應理工学部の数学過去問解説
下記に何年度かの慶應理工学部の過去問を解説していますのでご覧下さい。
慶應義塾大学理工学部に圧倒的な実力で合格できる専門対策をします
まずは資料請求・お問い合わせ・学習相談から!
早慶専門個別指導塾HIRO ACADEMIAには、慶應義塾大学専門として理工学部への圧倒的な合格ノウハウがございます。
少しでもご興味をお持ちいただいた方は、まずは合格に役立つノウハウや情報を、詰め込んだ資料をご請求ください。
また、慶應義塾大学理工学部に合格するためにどのよう勉強をしたらよいのかを指示する学習カウンセリングも承っています。学習状況を伺った上で、残りの期間でどう受かるかを提案いたしますので、ぜひお気軽にお電話いただければと思います。
⇒ 慶應義塾大学理工学部に合格したい方は、まずは当塾の資料をご請求ください。
























Published by