まず、N=24について考えてみます。
N=24=![]() で、約数をすべて列挙すると、{1,2,3,4,6,8,12,24}で約数の個数は、8コで約数すべての和は60です。
で、約数をすべて列挙すると、{1,2,3,4,6,8,12,24}で約数の個数は、8コで約数すべての和は60です。
次に、N=24・3=72について考えてみます。
N=![]() で、約数をすべて列挙すると、{1,2,3,4,6,8,9,12,18,24,36,72}で約数の個数は、12コで、約数のすべての和は195です。
で、約数をすべて列挙すると、{1,2,3,4,6,8,9,12,18,24,36,72}で約数の個数は、12コで、約数のすべての和は195です。
これら3つから、約数の個数と約数のすべての和について考えてみます。
・N=24のとき、{1,2,3,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() }で、
}で、
![]() は、1,3
は、1,3
![]() は2,
は2,![]()
![]() は
は![]() ,
,![]()
![]() は
は![]() ,
,![]() に含まれていることが分かります。
に含まれていることが分かります。
つまり、![]() (0≦k≦3)は3の約数(1,3)とすべてかけられています。
(0≦k≦3)は3の約数(1,3)とすべてかけられています。
逆に、![]() は1,2,
は1,2,![]() ,
,![]()
![]() は3,
は3,![]() ,
,![]() ,
,![]() に含まれていますから、
に含まれていますから、![]() (0≦l≦1)は2の約数(1,2,
(0≦l≦1)は2の約数(1,2,![]() ,
,![]() )とすべてかけられています。
)とすべてかけられています。
以上から約数の個数はN=![]() のべき乗部分に注目して、(1+3)(1+1)=4・2=8コと求められます。
のべき乗部分に注目して、(1+3)(1+1)=4・2=8コと求められます。
和は、![]() となります。
となります。
・N=72=![]() のとき、{1,2,3,4,6,8,9,12,18,24,36,72}
のとき、{1,2,3,4,6,8,9,12,18,24,36,72}
つまり、{1,2,3,![]() }
}
_(傍線部)はN=24に含まれなかった約数です。_(傍線部)も![]()
すべてかけられているので先程と同様に考えると、(1+3)(1+1+1)=(1+3)(1+2)=4・3=12コで、和は![]() です。
です。
■JMO(日本数学オリンピック)の予選の問題ですが、約数の個数という面で楽しんで頂けないでしょうか?
結局、![]() をm=10,
をm=10,![]() (1≦i≦m)として、重複を2で割ったのが本問でした。
(1≦i≦m)として、重複を2で割ったのが本問でした。
ここまでくれば、アルゴリズムが見えてきますね。
![]() (1≦k≦m)を素数として、
(1≦k≦m)を素数として、![]() と表されたNの約数の個数は、
と表されたNの約数の個数は、![]()
約数の総和は、![]() と一般化できます。
と一般化できます。
さて、小手調べに以下の問題にとりくんでみよう!
▶問1
ある整数の約数をすべて足すと168になり、約数の逆数をすべて足すと、2.8になる整数を求めよ。(有名問題)
解 ![]() とする。
とする。
![]()
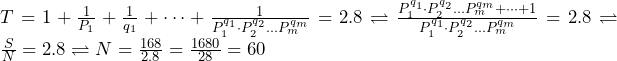
∴N=60…(答え)
■多項式と関係が深いです
ただの丸暗記だと、上の式変形は難しいかもしれませんが、この記事を読んだ皆さんなら、簡単に解けたのではないでしょうか?
▶問2
正の整数の組み(a,b)であって、a<b,ab=29!を満たし、かつaとbが互いに素であるようなものはいくつあるか。(2017JMO 予選2)
解 29以下の素数は、{1,2,3,5,7,11,13,17,23,29}の10コである。
まず、a=bと仮定すると,ab=29!⇄![]() =29!=28!・29で、29の要素は1つしかなく、平方数にならない。よって、a≠bである。
=29!=28!・29で、29の要素は1つしかなく、平方数にならない。よって、a≠bである。
29!=![]() とする。
とする。
![]() =x+y(1≦i≦10)、(1≦x≦
=x+y(1≦i≦10)、(1≦x≦![]() )として、たとえばaが
)として、たとえばaが![]() 、bが
、bが![]() を因数にもって、aとbが互いに素に矛盾するから、aとbは一方が
を因数にもって、aとbが互いに素に矛盾するから、aとbは一方が![]() をもつかどうかしかありえず、これは2通りである。
をもつかどうかしかありえず、これは2通りである。
各![]() (1≦i≦10)について同じことがいえるので、
(1≦i≦10)について同じことがいえるので、![]() 通りだが、これにはa>bも含まれている。
通りだが、これにはa>bも含まれている。
対称性(aとbをいれかえても変わらない)より、a<bとa>bの個数は同じだから求める個数は![]() 通り…(答)
通り…(答)
















Published by